Κληρονομικότητα

Διομήδης Σπινέλλης
Τμήμα Διοικητικής Επιστήμης και Τεχνολογίας
Οικονομικό Πανεπιστήμιο Αθηνών
dds@aueb.gr

Εισαγωγή

Συχνά μια σειρά κλάσεων αντικειμένων μπορεί να μοντελοποιηθεί με τη μορφή μιας ιεραρχίας.
Για παράδειγμα:
- Όλα τα μέλη της Πανεπιστημιακής Κοινότητας είναι φυσικά πρόσωπα και έχουν ως ιδιότητες το όνομα και το επώνυμό τους.
  - Οι φοιτητές έχουν ακόμα ως ιδιότητα τον αριθμό μητρώου τους (id) και το έτος που φοιτούν.
  - Όσοι έχουν σχέση εργασίας με το Πανεπιστήμιο έχουν ως ιδιότητα το μισθό τους.
    - Το διοικητικό προσωπικό έχει ως πρόσθετη ιδιότητα τον τομέα ευθύνης του.
    - Οι διδάσκοντες έχουν ως πρόσθετη ιδιότητα το τμήμα τους και τα μαθήματα που διδάσκουν.

Οι σχέσεις αυτών των κλάσεων μπορούν να παρασταθούν στο παρακάτω διάγραμμα.

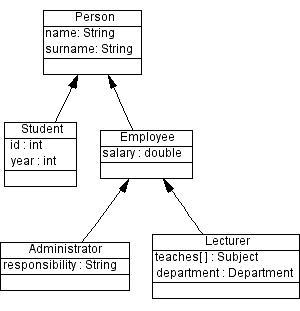
Κάθε κλάση κληρονομεί τις ιδιότητες της μητρικής της κλάσης.

Κληρονομικότητα σε κλάσεις

Η ιεραρχία των κλάσεων εκφράζεται στην Java με τον ορισμό μιας κλάσης που είναι υποκλάση (subclass) μιας άλλης κλάσης (που ονομάζεται βασική κλάση (base class)).
Η σύνταξη για τον ορισμό αυτό είναι της μορφής:
class υποκλάση extends βασική_κλάση {
// ...
Κάθε υποκλάση κληρονομεί (inherits) τις μεθόδους και τις ιδιότητες που έχουν οριστεί ως public στη βασική κλάση.
Η υποκλάση δεν έχει πρόσβαση στις μεθόδους και τις ιδιότητες που έχουν οριστεί ως private στη βασική κλάση.
Η υποκλάση μπορεί να ορίσει νέες ιδιότητες και μεθόδους και να υπερσκελίσει (override) ιδιότητες και μεθόδους που έχει ορίσει η βασική κλάση.
Έτσι, οι περισσότερες κλάσεις αντικαθιστούν τη μέθοδο toString() που επιστρέφει μια συμβολοσειρά που αντιστοιχεί στο περιεχόμενο ενός αντικειμένου και παρέχεται από την Java για όλα τα αντικείμενα με μια πιο εξειδικευμένη μέθοδο.
Μέσα από την κλάση μπορούμε να αναφερθούμε στη βασική κλάση με τον προσδιορισμό super.
Παράδειγμα:
import gr.aueb.dds.BIO;

class Shape {
        private int x, y;               // Position
        public void setPosition(int px, int py) {
                x = px;
                y = py;
        }
        public String toString() {
                return "Shape(" + x + ", " + y + ")";
        }
}

class Circle extends Shape {
        private int radius;
        public void setRadius(int r) {
                radius = r;
        }
        public String toString() {
                return super.toString() + ": Circle(" + radius + ")";
        }
}

class Rectangle extends Shape {
        private int height, width;
        public void setDimensions(int h, int w) {
                height = h;
                width = w;
        }
        public String toString() {
                return super.toString() + ": Rectangle(" + height + " x " + width + ")";
        }
}

class Test {
        static public void main(String args[])
        {
                Circle c = new Circle();
                Rectangle r = new Rectangle();

                r.setPosition(1, 2);
                r.setDimensions(50, 50);
                c.setPosition(3, 4);
                c.setRadius(10);
                BIO.println(r);
                BIO.println(c);
        }
}
Η παραπάνω διάταξη μπορεί να παρασταθεί σχηματικά ως εξής:
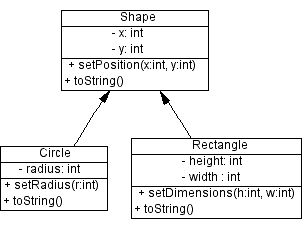
Μπορούμε να ορίσουμε μια άλλη κατηγορία μεθόδων και ιδιοτήτων με τον προσδιορισμό protected. Αυτές είναι προσβάσιμες από τις υποκλάσεις της κλάσης μας, αλλά όχι από άλλες συναρτήσεις. Παράδειγμα:
class Shape {
        private int x, y;               // Position
        protected int getX() { return x; }
        protected int getY() { return y; }
        public void setPosition(int px, int py) {
                x = px;
                y = py;
        }
        public String toString() {
                return "Shape(" + x + ", " + y + ")";
        }
}
Μια αναφορά (αντικείμενο) σε μια υποκλάση μπορεί αυτόματα να μετατραπεί σε αναφορά (αντικείμενο) της βασικής της κλάσης. Αυτό επιτρέπεται διότι κάθε αντικείμενο μιας υποκλάσης είναι (is a) και αντικείμενο της βασικής κλάσης. Το αντικείμενο συνεχίζει να διατηρεί τις ιδιότητες της υποκλάσης μετά τη μετατροπή και μπορεί να μετατραπεί πίσω στην ίδια υποκλάση με τη χρήση ρητού τελεστή μετατροπής (cast). Παράδειγμα:
static public void main(String args[])
{
        Rectangle r = new Rectangle();
        Shape s;

        r.setposition(1, 2);
        r.setdimensions(50, 50);
        s = r;
        s.setposition(10, 20);
        BIO.println(r);
        BIO.println(s);
        r = (Rectangle)s;
}

Δυναμική διεκπεραίωση

Οι υποκλάσεις μιας κλάσης μπορούν να αντικαταστήσουν μια μέθοδό της με μια που θα ορίσουν αυτές.
Όταν κληθεί η μέθοδος που έχει αντικατασταθεί από μια υποκλάση μέσω ενός αντικειμένου της βασικής κλάσης το οποίο έχει προέλθει από αντικείμενο κάποιας υποκλάσης τότε θα κληθεί η αντίστοιχη μέθοδος της υποκλάσης από την οποία έχει προέλθει το αντικείμενο.
Η δυνατότητα αυτή της δυναμικής διεκπεραίωσης (dynamic dispatch) επιτρέπει:
- το δυναμικό καθορισμό της συμπεριφοράς ενός αντικειμένου ανάλογα με την κλάση του κατά την εκτέλεση του προγράμματος,
- την αλλαγή της συμπεριφοράς μιας παλιάς κλάσης από μια νεώτερη (υποκλάση της) και
- την ενοποιημένη διαχείριση διαφορετικών αντικειμένων μέσω της βασικής τους κλάσης.
Η δυνατότητα αυτή προάγει τη Java από γλώσσα που υποστηρίζει τα αντικείμενα σε αντικειμενοστρεφή γλώσσα.

Αφηρημένες κλάσεις

Αν μια μέθοδος μιας κλάσης οριστεί με τον προσδιοριστή abstract και χωρίς σώμα τότε η συνάρτηση αυτή είναι ιδεατή (abstract) δηλαδή δεν έχει υλοποίηση στη συγκεκριμένη κλάση. Παράδειγμα:
abstract class document {
public abstract String identify();
}
Αν μια κλάση περιέχει (ή έχει κληρονομήσει) τουλάχιστον μια ιδεατή μέθοδο τότε και αυτή πρέπει να οριστεί με τον προσδιοριστή abstract και ονομάζεται ιδεατή (abstract).
Οι ιδεατές κλάσεις χρησιμοποιούνται μόνο για να ορίσουν γενικές έννοιες από τις οποίες εκπορεύονται συγκεκριμένες κλάσεις.
Σε αντικείμενα μιας ιδεατής κλάσης μπορούν να ανατεθούν αντικείμενα από μη ιδεατές υποκλάσεις της. Τα ίδια όμως τα αντικείμενα μιας ιδεατής κλάσης δεν μπορούν ποτέ να δημιουργηθούν αυτούσια.

Για παράδειγμα, ένας σχεδιασμός του πληροφοριακού συστήματος του Πανεπιστημίου μπορεί να ορίσει την ιδεατή κλάση person ως βασική κλάση για τις υποκλάσεις student, employee και visitor. Αν και δε θα μπορεί να ένα νέο αντικείμενο με βάση την αφηρημένη κλάση person, αυτή μπορεί να περιέχει ορισμένα βασικά χαρακτηριστικά όπως birth_date και να επιβάλει την υλοποίηση συγκεκριμένων μεθόδων όπως home_page_URL() ορίζοντάς τις ως ιδεατές.

Παράδειγμα

Το παρακάτω παράδειγμα ορίζει τη βασική κλάση Shape και τις υποκλάσεις της Circle και Rectangle. Η μέθοδος area μπορεί να οριστεί για τις υποκλάσεις και κατά την εκτέλεση του προγράμματος να εκτελεστεί η σωστή έκδοσή της. Η συνάρτηση toString της Shape εκμεταλλεύεται τη δυνατότητα αυτή και μπορεί να κληθεί (και να δουλέψει σωστά) με όρισμα οποιαδήποτε από τις υποκλάσεις της shape.

import gr.aueb.dds.BIO;

abstract class Shape {
        private double x, y;            // Position
        protected double getX() { return x; }
        protected double getY() { return y; }
        public void setposition(double px, double py) {
                x = px;
                y = py;
        }
        public abstract double area();
        public String toString() {
                return "Shape(x=" + x + ", y=" + y + ", area=" + area() + ")";
        }
}

class Circle extends Shape {
        private double radius;
        public void setradius(double r) {
                radius = r;
        }
        public double area() {
                return 2 * Math.PI * radius * radius;
        }
        public String toString() {
                return super.toString() + ": Circle(" + radius + ")";
        }
}

class Rectangle extends Shape {
        private double height, width;
        public void setdimensions(double h, double w) {
                height = h;
                width = w;
        }
        public double area() {
                return height * width;
        }
        public String toString() {
                return super.toString() + ": Rectangle(" + height + " x " + width + ")";
        }
}

class Test {
        static public void main(String args[])
        {
                Circle c = new Circle();
                Rectangle r = new Rectangle();
                Shape s[] = new Shape[2];

                s[0] = r;
                r.setposition(1, 2);
                r.setdimensions(50, 50);

                s[1] = c;
                c.setposition(3, 4);
                c.setradius(10);
                for (int i = 0; i < s.length; i++)
                        BIO.println(s[i]);
        }
}

Το παραπάνω πρόγραμμα θα τυπώσει:

Shape(x=1.0, y=2.0, area=2500.0): Rectangle(50.0 x 50.0)
Shape(x=3.0, y=4.0, area=628.3185307179587): Circle(10.0)

Ασκήσεις

Να υλοποιηθούν σε Java οι κλάσεις AndGate, OrGate, NotGate. Οι κλάσεις αυτές θα προσομοιάζουν τις αντίστοιχες λογικές πύλες. Κάθε κλάση να έχει μεθόδους που να θέτουν τις εισόδους (π.χ. setA, setB) και μέθοδο που να επιστρέφει την τιμή της εξόδου (π.χ. getOutput).
Με τη χρήση των παραπάνω κλάσεων (και μόνο) να υλοποιήσετε μια κλάση που να προσομοιάζει έναν ημιαθροιστή. Η κλάση αυτή να έχει μεθόδους που να θέτουν τις δύο εισόδους και μεθόδους που να επιστρέφουν το άθροισμα (getSum) και το κρατούμενο (getCarryOut).
Να γράψετε ένα πρόγραμμα σε Java που να τυπώνει τους πίνακες αλήθειας για τις παραπάνω κλάσεις.
(Προαιρετικά) Με τη χρήση των παραπάνω κλάσεων να υλοποιήσετε μια κλάση που να προσομοιάζει έναν πλήρη αθροιστή. Η κλάση αυτή πρέπει να έχει μεθόδους που να θέτουν τις δύο εισόδους και το κρατούμενο εισόδου (setCarryIn) καθώς και μεθόδους που να επιστρέφουν το άθροισμα και το κρατούμενο εξόδου. Με τη χρήση του πλήρη αθροιστή και τους τελεστές bit της Java μπορεί να υλοποιηθεί μια κλάση αθροιστή ακεραίων αριθμών (wordadder) με τον παρακάτω τρόπο:
/*
* wordadder.java
*
* D. Spinellis, February 2000, December 2001
*/

import gr.aueb.dds.BIO;

class WordAdder {
        private int a, b;
        public void setA(int v) { a = v;}
        public void setB(int v) {b = v;}
        public int getSum() {
                FullAdder fa[] = new FullAdder[32];
                int i, bit;
                int result = 0;

                for (i = 0; i < 32; i++)
                        fa[i] = new FullAdder();

                fa[0].setCarryIn(false);
                // bit is the bit position to add
                for (i = 0, bit = 1; i < 32; bit <<= 1, i++) {
                        fa[i].setA((a & bit) != 0);
                        fa[i].setB((b & bit) != 0);
                        // Propagate carry
                        if (i < 31)
                                fa[i + 1].setCarryIn(fa[i].getCarryOut());
                        // Merge adder output into result
                        if (fa[i].getSum())
                                result |= bit;
                }
                return (result);
        }

        // Test harness
        public static void main(String args[]) {
                int a, b;
                WordAdder wa = new WordAdder();

                BIO.print("a=");
                wa.setA(a = BIO.readInt());
                BIO.print("b=");
                wa.setB(b = BIO.readInt());
                BIO.println(a + " + " + b + " = " + wa.getSum());
        }

}

Δοκιμάστε το!

Βιβλιογραφία

Γιώργος Λιακέας Εισαγωγή στην Java. σ. 141-152 Εκδόσεις Κλειδάριθμος 2001.

K. N. King. Java Programming: from the Beginning, pages 85–117. W. W. Norton & Company, New York, NY, USA, 2000.

Περιεχόμενα