Coding for Numbers
Diomidis Spinellis
Numerical Recipes in C++: The Art of Scientific Computing, 2nd edition by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery, Cambridge University Press, 2002, ISBN 0-521-75033-4, 1,002 pp., US$70.00.
Programs that perform sophisticated numberical calculations critically depend on the algorithms they use. Even if you obtain the correct requirements, come up with a brilliant architectural design, and write maintainable and efficient code, it’s the underlying algorithm that will often make or break your application. The “Numerical Recipes” series of books distills in an accessible format the background theory, solid algorithms, and working programs for performing all but the most advanced numerical analysis tasks needed for scientific computing and many engineering applications.
The book series has grown from the 1988 original Fortran-based book to include separate versions for Fortran 77, Fortran 90 (dealing with parallel computing), C, and C++. The second edition of Numerical Recipes in C++: The Art of Scientific Computing is more than 50 percent larger than the first and includes more than 300 separate algorithms.
Authoritative guidelines for complex calculations
The book’s chapters detail linear algebraic equation solutions, interpolation and extrapolation, and functions’ evaluation and minimization. They also cover Monte Carlo methods, root finding, Eigensystems, the Fourier transform and its applications, data modeling, boundary value problems, ordinary and partial differential equations, and integral equations. The book also contains other algorithms that scientists might find useful, such as those dealing with the statistical description of data, random numbers, compression, coding, and arbitrary precision arithmetic. The book’s range of topics is extremely wide; hopefully, the next edition’s minimization techniques discussion will include additional stochastic methods apart from simulated annealing, such as genetic algorithms and tabu search techniques.
Anyone performing calculations more complex than integer
addition and subtraction is likely to benefit from this book’s prescriptive and
sometimes wry-humored guidelines. If for example you think that ![]() is the way to find
the Euclidean distance between two points, you’d better rush out for a copy of
the book. The authors label this formula as “bad!” and explain that it will
overflow if any of the numbers is as large as the square root of the largest
representable number. Instead, they propose that you use:
is the way to find
the Euclidean distance between two points, you’d better rush out for a copy of
the book. The authors label this formula as “bad!” and explain that it will
overflow if any of the numbers is as large as the square root of the largest
representable number. Instead, they propose that you use:
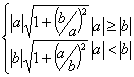
In most cases, the authors don’t formally examine the proposed algorithms’ stability and accuracy properties—doing so would easily quadruple the book’s size with minimal benefit to most readers. Instead, true to the book’s title, the authors offer tried-and-tested recipes that will make your scientific programming a success.
Major improvements
The second edition finally does away with the
Fortran-derived arrays and matrices indexed from Element 1 that were infesting
earlier editions and uses a number of C++ features to improve the algorithms’
presentation and value. Most importantly, the authors use a family of templated
objects to support a uniform implementation of variable-sized vectors and
matrices. You can easily adapt the provided containers’ minimal implementation
into a wrapper for the more full-featured matrix library you might be using. In
addition, the book’s code isolates all program elements in appropriate C++
namespaces; efficiently passes arguments to functions using C++ references;
uses the “const” keyword to identify function arguments that won’t be modified;
and declares small, heavily used functions as “inline.”
Unfortunately, the reader expecting to find the C++ object-oriented and generic programming features applied on the algorithms themselves will be severely disappointed. The authors present all algorithms as global functions, still named with cryptic 1960s Fortran-era, six-character identifiers: amotsa, bessk1, covsrt, erfcc, and frprmn. (They claim that this makes the functions easier to reuse in other applications, since the functions carry relatively little additional supporting baggage; the six-character identifiers maintain continuity and compatibility with the book’s widely used earlier editions. However, I was left wondering how the power of full-fledged generic programming, the C++ Standard Template Library’s containers, iterators, and algorithms, and the use of object-based information hiding, encapsulation, and inheritance could have been applied to the book’s substantial and important body of algorithmic knowledge. Given that the book will be heavily used by scientists of all fields for years to come, its failure to use the abstractions and methods that we, computing professionals, consider important software building blocks is a problem that our profession should face, explain, and address.
Diomidis Spinellis is an associate professor in the Department of Management Science and Technology at the Athens University of Economics and Business. Contact him at dds@aueb.gr.