Using Object-Oriented Design Metrics to Predict Software
Defects*
Marian JURECZKO,
Diomidis D. SPINELLIS
1.
Introduction
Many object-oriented design metrics have
been developed [1,3,8,17,24] to help in predict software defects or evaluate
design quality. Since a defect prediction model may give crucial clues about
the distribution and location of defects and, thereby, test prioritization,
accurate prediction can save costs in the testing process. Considerable
research has been performed on defect prediction methods; see the surveys by
Purao and Vaishnavi [22] and by Wahyudin et al. [25], unfortunately few results
appear at statistically significant level. Therefore, further empirical
validation is necessary to prove the usefulness of the metrics and software
prediction models in industrial practice.
Our study was made possible through the creation of a new
metric calculation tool. There are many tools that calculate
object-oriented metrics. What is the reason to create another one? In fact the
situation is not so perfect. The available programs are either extremely
inefficient (sometimes they do not work with big software projects at all), not
available as open source and therefore difficult to reason about their results,
or incomplete — the set of calculated metrics is not wide enough. It is
extremely hard to find a tool that calculates all metrics from the Chidamber
and Kemerer (C&K) metrics suite [3]. Having both, C&K and QMOOD metrics
suites [1] in one tool is even rarer, and according to the authors' knowledge
there is no other tool, that calculates metrics suggested by Tang et al. [24].
Ckjm calculates metrics that have been recommended as good quality indicators.
There are several works that investigate the C&K metric suite and that have
empirically proven their usability in quality or defect prediction [2, 10, 11,
20]. There are recommendations about QMOOD metrics suite [1, 20] and the
quality oriented extension of C&K [24] too. Ckjm does not offer a GUI and
its focus is not on elaborate diagrams but on efficient calculation of metrics.
Ckjm is an open source project, thus it is free of charge. Finally, Ckjm is a
mature tool. This paper presents a new version of the tool substantially expanding
a previous version (v 1.8)
which evaluated a smaller set of metrics. The new version is a quality oriented
extension and calculates many additional metrics that have been recommended as
good quality indicators.
The paper is organized as follows: In Section 2 the
motivation and goals are provided. In Section 3 related works are described.
Section 4 presents the suite of OO metrics that are calculated by ckjm. The
experiment is shown in Section 5. This includes description of investigated
projects and methods of data acquiring in Section 5.1, conducted statistical
analysis in Section 5.2 and potential threats in Section 5.3. Section 6
contains results of the experiment. Conclusions and future research are in
Section 7.
2.
Motivation and goals
Testing of software systems is an activity that consumes time
and resources. Applying the same testing effort to all modules of a system is
not the optimal approach, because the distribution of bugs among individual
parts of a software system is not uniform. Therefore, testers should be able to
identify fault-prone classes. With such knowledge they would be able to
prioritize the tests and therefore, work more efficiently. The availability of
adequate software defect prediction models is, thus, vital. This task can be performed by tools,
like ckjm, which is designed to help in quality assurance by calculating metrics
that can be used to predict software defects.
The main goal of this research is to construct software
defect prediction models. The metrics calculated by ckjm are used as the model
input. Therefore, the model constructing process allows deciding whether the
calculated metrics are usable as defect predictors. The estimated number of
defects for a Java class is the model output. The model output may be used to
select classes where the estimated number of defects is on high level.
According to Weyuker et al. [21,26,27,28] typically 20% of files contain
upwards of 80% of defects. Testers with a good defect predicator should be able
to reduce their test effort by testing only 20% of files (Java classes) and
they still should be able to find most of the defects (80%). Models constructed
in this research are evaluated by counting the percentage of Java classes that
must be tested in order to find 80% of the defects.
The collecting of
data, that was required to construct the software defect prediction models,
gave an opportunity to investigate a hypothesis about factors that influence at
defect prediction mechanism. There are works [5,6,13,14,19] where class or module
size has been pointed as an important factor in defect prediction. 44 models,
that ignore the class size factor and 88 models that use the class size factor
have been created in order to test if the class size factor has statistically
significant influence on defect prediction accuracy. There are so many models
and only 16 software projects because several versions of each project have
been investigated.
3.
Related work
Considerable research has been performed on software metrics;
see Kan's monograph [12], survey by Purao and Vaishnavi [22], and the
references therein. Some of the metrics has been shown to be useful for
predicting the fault-proneness of classes and for building the software defect
prediction models [1,2,4,9,10,11,15,19,20,21,23,24,26,27, 28,29]. There are
also several papers where the Pareto analysis has been used to evaluate the
models ability of identifying the fault-prone classes, modules or files.
Weyuker et al. found 76-93% of the faults in 20% of the files that had been
selected by defect prediction model, by using the negative binomial regression
[21] and 68-85% of the faults by using the recursive partitioning [26]. Further,
the models were simplified in order to make them more generic, what resulted in
founding 50-92% of the fault in 20% of the files. Denaro and Pezze [4] used
logistic regression models to identify fault-prone modules. They reported that
their best model required about 50% of the modules to be investigated in order
to find 80% of the software faults. They used data collected from Apache v. 1.3
and they assessed the model on Apache v. 2.0. Succi et al. [23] used C&K
metrics suite as well as software size to find fault-prone classes. They have
investigated two software projects, both written in C++. They reported, that
their required 43-48% of classes to be analyzed in order to cover 80% of the
defects.
According to the authors' knowledge, few works has been done
on the use of class size for defect prediction. Some interesting observations
are the followings. Fenton and Neil [6] described the phenomenon, that larger
modules may have lower defect densities. Koru and Liu [13] discovered that the
predictability was worse for subsets that included many small components and
they gave some practical hints that explain how the defect prediction models
should be constructed with respect to their findings [14]. Their advice is that
data sets are stratified according to the module size in order to facilitate prediction
of defects on these data subsets. Mende and Koschke [19] created defect prediction
models, that were based only on the module size measured in Line of Code (LoC).
The results were surprisingly well. The outputs of their models were strongly
correlated with the actually data. The Spearman's correlation coefficient
varied between 0.41 and 0.9. El Emam et al. [5] investigated whether there is a
confounding effect of class size measured in Line of Code (LoC). They
considered the C&K metrics, and a subset of the Lorenz and Kidd [16]
metrics. Their findings indicate that the class size should be considered in
the defect prediction models. However El Emam et al. investigated only one
software project.
4.
The metrics
The set of metrics that ckjm is able to calculate are listed
in Table 1 and have been defined according to the metric importance in defect
prediction. All metrics, except McCabe's Cyclomatic Complexity (CC), are class
size metrics.
Table 1. Metrics definitions.
|
Metric Name
|
Definition
|
Source
|
|
Weighted methods per class (WMC)
|
The value of the WMC is equal to the number of methods in
the class (assuming unity weights for all methods).
|
C&K [3]
|
|
Depth of Inheritance Tree (DIT)
|
The DIT metric provides for each class a measure of the
inheritance levels from the object hierarchy top.
|
C&K [3]
|
|
Number of Children (NOC)
|
The NOC metric simply measures the number of immediate
descendants of the class.
|
C&K [3]
|
|
Coupling between object classes (CBO)
|
The CBO metric represents the number of classes coupled to
a given class (efferent couplings and afferent couplings). This couplings can
occur through method calls, field accesses, inheritance, method arguments,
return types, and exceptions.
|
C&K [3]
|
|
Response for a Class (RFC)
|
The RFC metric measures the number of different methods
that can be executed when an object of that class receives a message.
Ideally, we would want to find for each method of the class, the methods that
class will call, and repeat this for each called method, calculating what is
called the transitive closure
of the method call graph. This process can however be both expensive and
quite inaccurate. Ckjm
calculates a rough approximation to the response set by simply inspecting
method calls within the class method bodies. The value of RFC is the sum of
number of methods called within the class method bodies and the number of
class methods. This simplification was also used in the Chidamber and
Kemerer's [3] description of the metric.
|
C&K [3]
|
|
Lack of cohesion in methods (LCOM)
|
The LCOM metric counts the sets of methods in a class that
are not related through the sharing of some of the class fields. The original
definition of this metric (which is the one used in ckjm) considers all pairs of class methods.
In some of these pairs both methods access at least one common field of the
class, while in other pairs the two methods do not share any common field
accesses. The lack of cohesion in methods is then calculated by subtracting
from the number of method pairs that do not share a field access the number
of method pairs that do.
|
C&K [3]
|
|
Lack of cohesion in methods (LCOM3)
|
|
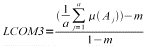
|
m - number of methods in a class
a - number of attributes in a class
µ(A) - number of methods that access the attribute
A
|
|
Henderson-Sellers [8]
|
|
Afferent couplings (Ca)
|
The Ca metric represents the number of classes that depend
upon the measured class.
|
Martin [17]
|
|
Efferent couplings (Ce)
|
The Ca metric represents the number of classes that the
measured class is depended upon.
|
Martin [17]
|
|
Number of Public Methods (NPM)
|
The NPM metric simply counts all the methods in a class
that are declared as public. The metric is known also as Class Interface Size
(CIS)
|
QMOOD [1]
|
|
Data Access Metric
(DAM)
|
This metric is the ratio of the number of private
(protected) attributes to the total number of attributes declared in the
class.
|
QMOOD [1]
|
|
Measure of Aggregation (MOA)
|
This metric measures the extent of the part-whole relationship,
realized by using attributes. The metric is a count of the number of class
fields whose types are user defined classes.
|
QMOOD [1]
|
|
Measure of Functional Abstraction (MFA)
|
This metric is the ratio of the number of methods
inherited by a class to the total number of methods accessible by the member
methods of the class. The constructors and the java.lang.Object (as parent)
are ignored.
|
QMOOD [1]
|
|
Cohesion Among Methods of Class (CAM)
|
This metric computes the relatedness among methods of a
class based upon the parameter list of the methods. The metric is computed
using the summation of number of different types of method parameters in
every method divided by a multiplication of number of different method
parameter types in whole class and number of methods.
|
QMOOD [1]
|
|
Inheritance Coupling
(IC)
|
This metric provides the number of parent classes to which
a given class is coupled. A class is coupled to its parent class if one of
its inherited methods functionally dependent on the new or redefined methods
in the class. A class is coupled to its parent class if one of the following
conditions is satisfied:
· One of its
inherited methods uses an attribute that is defined in a new/redefined
method.
· One of its
inherited methods calls a redefined method.
· One of its
inherited methods is called by a redefined method and uses a parameter that
is defined in the redefined method.
|
Tang [24]
|
|
Coupling Between Methods (CBM)
|
The metric measures the total number of new/redefined
methods to which all the inherited methods are coupled. There is a coupling
when at least one of the given in the IC metric definition conditions is
held.
|
Tang [24]
|
|
Average Method Complexity (AMC)
|
This metric measures the average method size for each
class. Size of a method is equal to the number of Java binary codes in the
method.
|
Tang [24]
|
|
McCabe's cyclomatic complexity (CC)
|
CC is equal to number of different paths in a method
(function) plus one. The cyclomatic complexity is defined as:
|
CC = E – N + P
|
E - the number of edges of the graph
N - the number of nodes of the graph
P - the number of connected components
|
CC is the only method size metric. The constructed models
make the class size predictions. Therefore, the metric had to be converted to
a class size metric. Two metrics has been derived:
·
Max(CC) - the greatest value of CC among methods of
the investigated class.
·
Avg(CC) - the arithmetic mean of the CC value in the
investigated class.
|
McCabe [18]
|
|
Lines of Code (LOC)
|
The LOC metric based on Java binary code. It is the sum of
number of fields, number of methods and number of instructions in every
method of the investigated class.
|
|
5.
Study design
There are many guidelines for constructing defect prediction
models [6,7,25]. The approach that has been used in this paper does not follow
all the recommendations found in the literature. Some simplifications have been
made. According to Lessmann et al. [15] simple algorithms are not significantly
worse than the sophisticated data processing techniques. Thus the models output
may be not as accurate as it is possible but still usable and helpful in the
testing process.
5.1 Data sourceS
The data about software projects metrics and defects has been
collected from source code repositories. The ckjm tool has been used to
calculate the metrics. Another tool, called BugInfo, has been prepared to
identify defects. BugInfo analyses the logs from source code repositories
(Subversion or CVS) and according to the log content decides if a commit is a bugfix. Each of the projects
had been investigated in order to identify bugfixes commenting guidelines that
were used in the source code repository. The guidelines were formalized in
regular expressions. Buginfo compares the regular expressions with comments of
the commits. When a comment fits to a
regular expression, BugInfo increments the defect count for all classes that
have been modified in the commit.
The following projects have been investigated (project size
is the average number of classes):
Forrest
(http://forrest.apache.org/). The Forrest software is a publishing framework
that transforms input from various sources into a unified presentation in one
or more output formats. Size = 34.
POI
(http://poi.apache.org/). The POI project consists of APIs for manipulating various
file formats based upon Microsoft's OLE 2 Compound Document format, and Office
OpenXML format, using pure Java. Size = 421.
Synapse
(http://synapse.apache.org/). Synapse is a simple, lightweight and high performance
Enterprise Service Bus (ESB) from Apache. Synapse has support for HTTP, SOAP,
SMTP, JMS, FTP and file system transports, Financial Information eXchange (FIX)
and Hessian protocols for message exchange as well as first class support for
standards such as WS-Addressing, Web Services Security (WSS), Web Services Reliable
Messaging (WSRM), efficient binary attachments (MTOM/XOP). Size = 220.
Xalan-Java
(http://xml.apache.org/xalan-j/). Xalan is an XSLT processor for transforming
XML documents into HTML, text, or other XML document types. It implements XSL
Transformations (XSLT) Version 1.0 and XML Path Language (XPath) Version 1.0.
Size = 1043.
PBeans
(http://pbeans.sourceforge.net/). pBeans is a Java persistence layer and an
object/relational database mapping (ORM) framework. Size = 48.
Xerces
(http://xerces.apache.org/xerces-j/). Xerces is a Parser that supports the XML
1.0 recommendation and contains advanced parser functionality, such as support
for XML Schema 1.0, DOM level 2 and SAX version 2. Size = 484.
Ant
(http://ant.apache.org/). Ant is a well known Java-based, shell independent
build tool. Size = 488.
Ivy
(http://ant.apache.org/ivy/). Ivy is a dependency manager focusing on
flexibility and simplicity. Size = 311.
Camel
(http://camel.apache.org/). Apache Camel is a powerful open source integration
framework based on known Enterprise Integration Patterns with powerful Bean Integration.
Size = 894.
Log4j
(http://logging.apache.org/log4j/). Log4j is a well known logging framework.
Size = 187.
Lucene
(http://lucene.apache.org/). Lucene provides Java-based indexing and search
technology, as well as spellchecking, hit highlighting and advanced analysis/tokenization
capabilities. Size = 402.
There are five proprietary software projects too. All of them
are custom build solutions and all of them were successfully installed in the
customer environment. Their sizes are as follows: prop-1 size = 3954; prop-2
size = 2138; prop3 size = 2218; prop-4 size = 2860; prop-5 size = 3574.
5.3 Data analysis method
The main goal of this study is to empirically validate
metrics calculated by the ckjm tool whether those metrics are useful for
predicting fault-prone classes. A class is said to be fault-prone if it has at
least one defect. The defect is identifying according to the history from the
source version control system. When a class has been changed and the change has
been marked as defect (bug) fix, the count of the defects for the class will be
incremented.
The second goal of this study is to investigate whether class
size is a relevant factor in the defect prediction models. This lead to the
formulation of the following quantifiable hypothesis to be tested:
· H0 WMC – There
is no difference in the accuracy of the defect prediction models between model
using the WMC metric as the class size factor and model ignoring the class size
factor.
· HA WMC – There
is a difference in the accuracy of the defect prediction models between model
using the WMC metric as the class size factor and model ignoring the class size
factor.
· H0 LOC – There
is no difference in the accuracy of the defect prediction models between model
using the LOC metric as the class size factor and model ignoring the class size
factor.
· HA
LOC – There is a difference in the accuracy of the defect prediction
models between model using the LOC metric as the class size factor and model
ignoring the class size factor.
Model accuracy is the percentage of classes that have to be
investigated in order to find 80% of the defects. The classes are investigated
in the order of decreasing estimated number of defect. The estimation is made
by the defect prediction model. Each of the investigated software projects has
at least two versions (external releases). The model constructed on the project
version i-1 is always assessed on the version i. The data about
version i-1 is always available during version i
development. Therefore, the
assessment method suits very well to the software development practice.
The following steps are performed in order to construct a
defect prediction model:
1. Correlation matrix with
all metrics and the number of defects is created. The Pearson correlation coefficient
(r) is used.
2. Highly
Correlated metrics are identified (r>0.8
and correlation statistically significant with a=0.05).
The highly correlated metrics that are lower correlated with the number of
defects are eliminated from further calculations. Example: rRFC,CBO=0.9, rRFC,Defect=0.69, rCBO,Defect=0.77 – the RFC metric
will be eliminated.
3. Stepwise linear regression is used
to construct the model. All no eliminated metrics are used as independent
variables. The number of defects is used as the dependent variable.
For models using the class size factor, the input data is
divided into two sets according to the value of the class size factor. We
assign small classes in the first set and big classes in the
second set. The above steps are performed for each set separately.
The hypotheses are evaluated by the parametric t-test.
Following general assumptions should be checked in order to use a parametric
test: level of measurement (the variables must be measured at the interval or
ratio level scale), independence of observations, homogeneity of variance and
the normal distribution of the sample. The homogeneity of variance is checked
by Levene's test. The assumption that the sample came from a normally
distributed population is tested by the Shapiro-Wilk and Kolmogorov-Smirnov
tests.
5.4 Threats to validity
A number of limitations that may compromise to some extent
the quality of the results of this study are listed below.
· It is possible that there
are mistakes in the defect identification. The comments in the source code
version control system are not always well written and, therefore, it was
sometimes very hard to decide whether a change is connected with a defect or
not.
· Metrics from the revision r1
and defects fixed in revisions (r1;r2)
are taken to build the defect prediction model. Subsequently, the model takes
(as input) metrics from the revision r2 and the model is used
to predict defects in (r2;r3). Therefore,
all information about the classes (and their defect), that have been created in
the period (r1;r2) are ignored during model
creation because those classes did not exist in the r1 revision.
·  The defects are assigned to versions
according to the bugfix date. It could be probably better to assign a defect to
the version, where the defect has been found, but unfortunately, the source
code version control system does not contain such information.
The defects are assigned to versions
according to the bugfix date. It could be probably better to assign a defect to
the version, where the defect has been found, but unfortunately, the source
code version control system does not contain such information.
· We were not able to track
operations like changing class name or moving class between packages. Therefore,
after such a change, the class is interpreted as a new class.
6. Results
 The details of creating the defect prediction
models would be impossible to present in the space provided. The results of
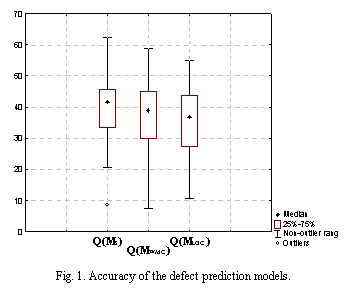
applying models are described on Figure 1. 8.57-62.27% of classes (mean (m) = 39.216; standard deviation (s) = 11.568) have to be investigate in order
to find 80% of defects when the simple models (Ms) are used. For the
models with the class size factor the results are as follows: 7.57-58.93% (m=37.433; s=10.258)
of classes have to be investigated according to the WMC based models (MWMC),
and 10,56%-54,93% (m=36.086; s=10,435) according to the LOC based models
(MLOC). Please notice that the Forrest project has been investigated
only with the simple model and the result, which has been obtained for this
project, is below the mean value. The project was too small to be investigated
with more sophisticated models. The Forrest project has been removed from the
sample before hypotheses testing.
The details of creating the defect prediction
models would be impossible to present in the space provided. The results of
applying models are described on Figure 1. 8.57-62.27% of classes (mean (m) = 39.216; standard deviation (s) = 11.568) have to be investigate in order
to find 80% of defects when the simple models (Ms) are used. For the
models with the class size factor the results are as follows: 7.57-58.93% (m=37.433; s=10.258)
of classes have to be investigated according to the WMC based models (MWMC),
and 10,56%-54,93% (m=36.086; s=10,435) according to the LOC based models
(MLOC). Please notice that the Forrest project has been investigated
only with the simple model and the result, which has been obtained for this
project, is below the mean value. The project was too small to be investigated
with more sophisticated models. The Forrest project has been removed from the
sample before hypotheses testing.
The assumptions that variables are
measured at the interval or ratio level and that the observations are
independent of one another are met. The assumption of homogeneity of variance
has been tested using Levelene's test. The test was not significant in both
cases (pS,WMC=0.768, pS,LOC=0.952), so we accept the null
hypothesis, that the population variances are equal. The assumption of
normality has been tested using the Kolmogorov-Smirnov and the Shapiro-Wilk
tests. The assumption of normality has not been violated: MS - S-W
(W=0.983, p=0.767), K-S (d=0.094, p=0.2); MWMC - S-W (W=0.981,
p=0.693), K-S (d=0.081, p=0.2); MLOC - S-W (W=0.976, p=0.482), K-S
(d=0.097, p=0.2).
Since
p>0.05 (probability level in tab. 3), there are no reasons to reject the H0
WMC or the H0 LOC hypothesis. So we can conclude
that the size factor did not significantly affect the defect prediction model
accuracy. According to fig. 1 models with the size factor give better predictions,
but the size factor based improvements are not statistically significant.
7.
Conclusions and future research
An analysis of the calculated metrics has been used to
construct defect prediction models. The models have been assessed on five
proprietary and eleven open source projects. Each time, a model constructed
according to the data from version i of a project has been assessed by
predicting the defects in version i+1 of the project. The analysis
showed that by applying simple regression models with the class size factor we
were able to find 80% of defects in 10.56% to 54.93% (m=36.086; s=10.435) of
the classes. Therefore, one could be able to save considerable costs in the
testing process by testing only 36% of the classes (the mean value) and still
finding most of the defects (80%). Using more sophisticated regression models
may lead to even better results; see Weyuker et al. [26,27,28] and the negative
binomial model. This is the primary contribution of the research. Another
contribution of the paper is an empirical study of usefulness of the class size
factor in the defect prediction models. Two metrics have been considered as the
class size factors: WMC (Weighted Methods per Class) and LOC (Lines of Code).
The WMC based models were slightly and the LOC based models were clearly better
as the simple models (without
class size factor), but the difference was statistically significant
neither in the case of WMC based models, nor in the case of LOC based models.
There are a number of factors (except the class size) that
may be relevant in defect prediction. The collected metrics will be used in
further researches, where we would like to try to identify the factors and
investigate whether they have statistically significant influence on defect
prediction. The number of investigated projects may be to small to perform some
of the analyses, especially increasing the sample size may show statistically
significance of the class size factor. Therefore data about further software
projects will be collected.
A simple regression model has been used in the presented
research. Using more sophisticated regression models, like the negative
binomial regression model, may be a better alternative. There are plans to
evaluate more sophisticated models to see how they will work, especially in
comparison wit the simple models.
We finish by noting the importance of conducting reproducible
empirical research studies. The researchers typically make many decisions in
order to study the software metrics. Therefore, the main way to make research
on software metrics reproducible is to make the collected metrics publicly accessible.
Therefore, we are going to place the collected metrics online at
http://purl.org/MarianJureczko/MetricsRepo.
Acknowledgements
The authors are very grateful to the Capgemini Polska Company
that allowed analyzsing five of their proprietary
projects. Thus, the research has been better validated - authors could use not
only open source, but also industrial projects.
References
[1] BANSIYA J., and DAVIS C. G., A
Hierarchical Model for Object-Oriented Design Quality Assessment. IEEE Trans. on Software Engineering,
28(1), 2002, 4-17.
[2] CATAL C., DIRI B. and OZUMUT B., An Artificial
Immune System Approach for Fault Prediction in Object-Oriented Software.
Proc. of Dependability of Computer Systems, 2007, 238-245.
[3] CHIDAMBER S. R. and KEMERER C. F.,
A metrics suite for object oriented design. IEEE Trans. on Software Engineering,
20(6), 476–493, 1994.
[4] DENARO G. and PEZZE M., An Empirical Evaluation
of Fault-Proneness Models. Proc. of International Conference on Software
Engineering (ICSE), 2002.
[5] EL ELMAM K., BENLARBI S. and GOEL N., The
Confounding Effect of Class Size on The Validity of Object-Oriented Metrics.
IEEE Trans. on Software
Engineering, 27(7), 2001, 630-650.
[6] FENTON N. E. and NEIL M., A Critique of Software
Defect Prediction Models. IEEE Trans. on Software Engineering, 25(5), 1999,
675-689.
[7] FENTON N. E., Software Measurement: A Necessary
Scientific Basis. IEEE Trans. on Software Engineering 20(3), 199-206, 1994.
[8] HENDERSON-SELLERS B., Object-Oriented Metrics,
measures of Complexity. Prentice Hall, 1996.
[9] JIANG Y., CUKIC B. and MA Y., Techniques for
evaluating fault prediction models. Empirical Software Engineering, 13(5),
2008, 561-595.
[10] JURECZKO M., Use of software metrics for finding
weak points of object oriented projects. Proc. of Metody i narzędzia
wytwarzania oprogramowania 133-144, 2007 (in Polish).
[11] JURECZKO M., Ocena jakości obiektowo
zorientowanego projektu programistycznego na podstawie metryk oprogramowania.
In: Inżynieria oprogramowania - metody wytwarzania i wybrane zastosowania, PWN,
364-377, 2008 (in Polish).
[12] KAN S. H., Metrics and Models in Software Quality
Engineering. Addison-Wesley, Boston MA, second edition, 2002.
[13] KORU A. G.,
and LIU H., An Investigation of the Effect of Module Size on Defect Prediction
Using Static Measures. Proc. of
PROMISE, 2005.
[14] KORU A. G. and LIU H., Building Effective
Defect-Prediction Models in Practice. IEEE Software 33(6), 2005, 23-28.
[15] LESSMANN S., BAESENS B., MUES C. and PIETSCH S., Benchmarking
Classification Models for Software Defect Prediction: A Proposed Framework and
Novel Findings. IEEE Trans. on Software Engineering 34(4), 2008, 485-496.
[16] LORENZ M. and KIDD J., Object-Oriented Software
Metrics. Prentice-Hall, 1994.
[17] MARTIN R., OO Design Quality Metrics - An
Analysis of Dependencies. Proc. of Workshop Pragmatic and Theoretical
Directions in Object-Oriented Software Metrics, OOPSLA’94, 1994.
[18] McCABE T. J.,
A complexity measure. IEEE Trans. on Software Engineering, 2(4),
1976, 308-320.
[19] MENDE T., KOSCHKE R., Revisiting the Evaluation
of Defect Prediction Models. Proc. of PROMISE, 2009.
[20] OLAGUE H. M., ETZKORN L. H., GHOLSTON S. and
QUATTLEBAUM S., Empirical Validation of Three Software Metrics Suites to
Predict Fault-Proneness of Object-Oriented Class Developed Using Highly
Iterative or Agile Software Development Processes. IEEE Trans. on Software
Engineering, 33(6), 2007, 402-419.
[21] OSTRAND T. J., WEYUKER E. J. and BELL R. M., Predicting
the Location and Number of Faults in Large Software Systems. IEEE Trans. on
Software Engineering, 31(4), 2005, 340-356.
[22] PURAO S. and VAISHNAVI V. K., Product metrics for
object-oriented systems. ACM Computing Surveys, 35(2): 191-221, 2003.
[23] SUCCI G., PEDRYCZ W., STEFANOVIC M. and MILLER J., Practical
assessment of the models for identification of defect-prone classes in
object-oriented commercial systems using design metrics. Journal of Systems
and Software 65(1), 2003, 1-12.
[24] TANG M-H., KAO M-H. and CHEN M-H, An
Empirical Study on Object-Oriented Metrics. Proc. of The Software Metrics Symposium,
1999, 242-249.
[25] WAHYUDIN D., RAMLER R. and BIFFL S., A framework
for Defect Prediction in Specific Software Project Contexts. Proc. of the
3rd IFIP CEE-SET, 2008, 295-308.
[26] WEYUKER E. J., OSTRAND T. J. and BELL R. M., Comparing
Negative Binomial and Recursive Partitioning Models for Fault Prediction.
Proc. of PROMISE, 2008.
[27] WEYUKER E. J., OSTRAND T. J. and BELL R. M., Adapting
a Fault Prediction Model to Allow Widespread Usage. Proc. of PROMISE, 2006.
[28] WEYUKER E. J., OSTRAND T. J. and BELL R. M., Do
too many cooks spoil the broth? Using the number of developers to enhance
defect prediction models. Empirical Software Engineering, 13(5), 2008,
539-559.
[29] ZHOU Y. and LEUNG H., Empirical Analysis of
Object-Oriented Design Metrics for Predicting High and Low Severity Faults.
IEEE Trans. on Software
Engineering, 32(10), 2006, 771-789.

 The defects are assigned to versions
according to the bugfix date. It could be probably better to assign a defect to
the version, where the defect has been found, but unfortunately, the source
code version control system does not contain such information.
The defects are assigned to versions
according to the bugfix date. It could be probably better to assign a defect to
the version, where the defect has been found, but unfortunately, the source
code version control system does not contain such information. The details of creating the defect prediction
models would be impossible to present in the space provided. The results of
applying models are described on Figure 1. 8.57-62.27% of classes (mean (
The details of creating the defect prediction
models would be impossible to present in the space provided. The results of
applying models are described on Figure 1. 8.57-62.27% of classes (mean (