
|
http://www.dmst.aueb.gr/dds/pubs/jrnl/1997-uProcessors-Cascade/html/casc.html This is an HTML rendering of a working paper draft that led to a publication. The publication should always be cited in preference to this draft using the following reference:
|
Abstract
The Cascade Vulnerability
Problem is a potential problem which must be faced when using
the interconnected accredited system approach of the Trusted Network
Interpretation. It belongs to a subset of the problem set that
addresses the issue of whether the interconnection of secure systems
via a secure channel results in a secure distributed system. The
Cascade Vulnerability problem appears when an adversary can take
advantage of network connections to compromise information across
a range of sensitivity levels that is greater than the accreditation
range of any of the component systems s/he must defeat to do so.
In this paper, we present the general Cascade vulnerability problem,
describe the basic properties of the most important detection
algorithms, conduct a brief comparative analysis, and present
a new approach based on simulated annealing for its correction.
Keywords: Cascade
Vulnerability Problem, Network & Open Distributed Systems
Security, Risk Analysis, Simulated annealing.
1. Introduction
The Cascade Vulnerability Problem was discussed in the Trusted Network Interpretation [1] of the Trusted Computer System Evaluation Criteria. According to [1] a Cascade Vulnerability Problem exists when a penetrator can take advantage of network connections to compromise information across a range of security levels that is greater than the accreditation range of any of the component systems s/he must defeat to do so.
In a distributed system with many
nodes and interconnections, the existence of a Cascade Vulnerability
Problem may not be obvious and can cause serious security problems.
In this paper we present the most effective algorithms - published
in the open literature - for the detection of the Cascade vulnerability
Problem and the identification of the paths along which the problem
exists. Then, we conduct a brief comparative analysis of the presented
algorithms. Finally, we outline the basic semantics of an algorithm
for the Restricted Cascade Correction Problem which proposes network
modifications for reducing the risk of Cascade Vulnerability.
2. The Cascade Vulnerability problem
The Cascade Vulnerability Problem belongs to a subspace of the problem set that addresses the issue of whether the interconnection of secure systems via a secure channel results in a secure distributed system. The term "secure system" is taken here to mean a system that has undergone not only a risk analysis evaluation with respect to the acceptable risk of operating the system, but a system security evaluation as well.
The assets of the system and the threats against each one of them are considered during the risk analysis review in order to identify the level of the security required. System security can be modelled as a function of many parameters, such as computer security, communications security, administrative security, personnel security, and physical security [2]. For implementation purposes all these parameters must be categorised into classes of countermeasures that reduce the system risks. Therefore, a system security evaluation assesses the effectiveness of the countermeasures which were finally selected for a specific system, at a given time.
The Cascade Vulnerability Problem appears in the subset of networks that cannot be treated as a single system. There are different reasons why networks cannot be viewed as a single system. The main reasons can be the large size of the network or the different administrative entities which may lead to different risk assessment methods. In any case, it is necessary for the administrators of any two systems that are to be interconnected to mutually agree that both systems are secure as stand-alone systems; that is, both administrators need to accept the risk assessment and the security evaluation methods which are used for both systems.
In summary, one can argue that [3] [4] the Cascade Vulnerability Problem appears when independent mutually recognised secure systems are interconnected by secure channels to create a distributed system which is not as secure as its parts.
As a typical example of the Cascade
Vulnerability Problem [1], let us consider two systems, as shown
in Figure 1. Host A is accredited for TS-Top Secret and S-Secret
information and all users are cleared to at least the Secret level.
Host B is accredited for S and C-Confidential and all users are
cleared to at least the Confidential level; finally, there is
a link at level S between the two systems.
System A
Figure 1. The generic Cascade Vulnerability
Problem.
While the risk of compromise in each of these systems is small enough to justify their use with two levels of information the system as a whole has three levels of information. This increases the potential harm that an adversary could cause, since s/he could downgrade the TS-level information in system A to S-level, send it to system B, and further downgrade the information to C-level therein.
The adversary has to defeat the protection mechanisms of both systems A and B, but that is an easier job than defeating the protection mechanisms of a single system trusted to protect the whole range from TS-level to C-level. The network connection has, in essence, created a Trusted Computing Base (TCB) with users cleared to at least the C-level with data on it at the TS-level.
In this way [5] the network connection
has invalidated the risk analysis that accredited the two systems,
because such a networked system must have a more secure architecture,
a TCB rating of B3, than either rating of the original individual
sub-systems TCB (i.e. B1 or B2, Figure 2).
Figure 2. Security Index Matrix for
Open Environments [6].
Let Rj(t) be the probability that both TCBs can be penetrated if the joint combination of two TCBs is subject to a total threat of t units or less. Changing variables and taking into account that the probability of two independent events occurring together is the product of their separate probabilities the value of Rj can be then computed as the convolution integral:
-
whose precise value in relation to the original RB2(x) is not intuitively obvious.

In Figure 3a and 3b the probability
density functions for RB2(t)
and of the Cascade Rj(t) are shown. It has been proven [7] that
Rj is approximately equal to R2B2 for the cascade of two B2 systems.
This means that the resistance to threat of a cascade of two B2
systems is approximately the same as, or even better than, that
of a B3 system.
3. Algorithms for Cascade Vulnerability
Detection
3.1 The Nesting and Cascade condition
The Nesting condition
The simplest approach for recognising a potential Cascade Vulnerability Problem is to test whether a network can or cannot face such a problem. This simple test is calling the nesting condition [1].
The nesting condition is true if
the accreditation ranges of each of the interconnected systems
are either:
Fulfilment of the nesting condition implies that there can be no Cascade Vulnerability Problem in the network at hand. However, there are many cases in the literature [5] where the nesting condition is not fulfilled, yet there is actually no Cascade Vulnerability Problem.
A possible solution when the problem
may exist is to eliminate certain network connections, either
physically or by means of end-to-end encryption. The later solution
allows hosts that need to communicate to do so, while eliminating
additional unnecessary cascading risk on the path from one host
to another.
The Cascading Condition
An attempt for a formal description of the Cascading Condition, which is more precise than the one described in [1], is presented in [5]. According to that, when we use a network, we know that it consists of some nodes h, and that every node has its accreditation range A(h). This A(h) consists of a set of sensitivity levels which, as a whole, form a lattice. Consequently, an accreditation range is a convex sublattice which is the formal notion corresponding to a range.
The protection regions are the pairs
(h,s), for each sensitivity level sA(h). A step
is an ordered pair of protection regions (h1,
s1), (h2, s2) such
that either:
In the second case, if also s1s2, then the information transfer is permitted by the enforced security policy in this specific node. A downgrade is a flow such that s1>s2.
A downgrade from s1
to s2
is always associated with a risk index R(s1,s2).
If s1s2,
then R(s1,s2)=0,
otherwise R(s1,s2)>0.
The risk index of any convex sublattice can be defined as the
least upper bound of all R(si,sj).
Two accreditation ranges - convex
sublattices are:
For a certain path (h1,s1), (h2,s2),..., (hn,sn), its net downgrade is R(s1,sn), and its difficulty is max(R(A(hi))), such that si>si+1.
According to the above formalism, a path is a Cascading path if its difficulty is at least as great as its net downgrade. Therefore, a network satisfies the Cascade condition if it has no Cascading paths at all.
In [5] one can find a program, written
in Edinburgh Prolog, that can identify all cascading paths based
on the previous formalism.
3.2 A heuristic procedure
The heuristic condition is a less conservative but much more complex heuristic that takes into account the connectivity of the network and the evaluation classes of the components. Given the goal of not allowing a risk greater than is recommended by the Environmental Guidelines, the heuristic procedure [1] has been developed to examine systems and determine whether they fall within the bounds prescribed by these Guidelines.
In formal terms the heuristic procedure is an approximate test for the Cascade Condition, described in the previous section. It should be noted that this procedure is not intended to be prescriptive: it is merely one way of examining the problem. It is obvious that the heuristic procedure - as every heuristic - has been derived through trial and error: it produces reasonable results and provides useful guidance to the prudence of interconnecting various systems.
In [1] an algorithm is described for determining whether or not a given network, composed of evaluated components meets the risk categories of the Environmental Guidelines. The algorithm is based on the idea of dividing a network into groups. The risk presented by any given group can be compared to the maximum allowed risk as defined by the Yellow Book for a system at the given evaluation class to determine if any community presents an unacceptable risk.
The steps for the heuristic procedure
are [1]:
If the Network Table Evaluation Class is greater than B1 then tables for each evaluation class lower than the class of the Network Table, must be produced down to tables for the C1 class. These tables will be produced for each evaluation class by first listing any one component whose evaluation class is less than or equal to the evaluation class for the table. Then add to the table all components that meet all of the following conditions:
The reader can find an analytical
application of the heuristic procedure in an example in [1].
3.3 Shortest path formulation
of the cascade problem
The formulation of the Cascade Vulnerability Problem as a Resource-Constrained Shortest Path Problem [3] [4] leads to an efficient algorithm for determining whether a network presents a Cascade Vulnerability Problem.
The resource-constrained shortest
path is based on three phases: Preprocessing, Shortest Path Calculation,
and Postprocessing.
In this approach the algorithm is flexible in two ways:
The time-complexity of the algorithm
is at most O(n'3)=O(a3n3),
where n' is the number of nodes in the expanded graph,
a is the number of security levels for data, and n
is the number of nodes in the network. The space-complexity of
the algorithm is O(n'2)=O(a2n2).
3.4 The Horton et al. Algorithm
An efficient algorithm for the detection of cascading vulnerability paths is presented in [9]. In this algorithm the interconnection network of trusted computer systems is modelled as a directed graph with n nodes and m edges. The nodes have a TCB rating associated with each other and represent the trusted subsystems. The edges represent the interconnection on which data can flow. The information needed to be associated with a node is the lowest user security level for which some user on the node is cleared, as well as the highest security level of labelled data at the node.
Each data path is represented by a directed edge or arc from the starting to the ending node of the path. With each arc a pair (d,u) is associated, where d is the security level of the data at the beginning of the path, and u the security level of the user at the end of the path. In a cascading vulnerability path the proposition u<d holds true.
The algorithm in [9] begins by creating arcs for each edge in the graph in which u and d are equal. The remaining part of the algorithm consists of two phases. In the first phase all possible legal paths through the network are found. A legal path is one for which du.
In the second phase the new arcs represent illegal data paths as well as legal data paths. The new step in this phase, is the answer of the question whether the TCB rating of node i allows the accreditation range of the arc(j, k). If it does, then the path corresponding to the new arc is not a cascading vulnerability path. If it does not, then the path from which this arc is constructed is a cascading vulnerability path. For determining the above the authors propose the use of the Floyd-Warshall shortest path algorithm [8].
A cascade vulnerability correction algorithm should include suggestions for these network modifications which eliminate or reduce the risk of cascade vulnerability. [9] supports the idea that an algorithm that solves the cascade vulnerability correction problem would also solve the vertex cover problem for planar graphs (which is known to be intractable). Based on the above, the cascade vulnerability correction problem appears to be NP-hard. The detection algorithm shows that the correction problem is in NP and therefore the problem is NP-complete. Thus, an efficient algorithm that would give the optimal solution is unlikely to be found.
It is only possible that by using
generalised techniques (e.g. ILP-Integer Linear Programming) a
reasonable initial network could be defined, with all known constraints
incorporated; this network could then be modified as unfulfilled
requirements are identified. Although solving integer linear programs
problems is also NP-complete, there are efficient techniques which
give acceptable solutions. The multiple-path problem can be stated
as an ILP [9] as follows:
p is a Cascading path in the network
n is a node in the network
s is the TCB rating for a system
cn,s is the cost of upgrading node n to rating s
n,s p means that upgrading node n to TCB rating s would correct path p
xn,s
is a variable that is either 1 (node n is to be upgraded
to TCB rating s) or 0 (node n is not to be upgraded
to TCB rating s).
Then
Minimise cn,s xn,s , subject to xn,s1, p
n,s n,sp
The basic disadvantage of Horton's
algorithm is that not all pairs of nodes connected by cascading
vulnerability paths are found. However, if all the pairs of nodes
connected by cascading vulnerability paths that are found are
corrected, then all the cascading vulnerability paths are corrected.
Any unreported cascading vulnerability paths will contain all
of some reported cascading path.
3.5 Algorithm comparative effectiveness
analysis
As stated above, the Horton algorithm has reduced time-complexity O(an3) as compared to O(a3n3) for the [3] algorithm. The space-complexity for the [9] algorithm is O(an2) as compared to O(a2n2) for the [3] [4] algorithm. In [10] the resistance of all paths in the network is calculated by a matrix computation which requires O(n3log2n) steps.
A problem common to [3] [4] [9] is the following: if there are multiple cascading vulnerability paths between a pair of nodes, then only one of the paths will be detected using the straightforward version of the corresponding algorithm.
However, the [9] algorithm does not
handle partially-ordered security levels as the [3] [4] [10] algorithms
do.
4. A Simulated Annealing approach
The computational complexity of the above algorithms and, in particular, the time-complexity of the shortest path algorithm led us towards examining the applicability of simulated annealing as the cascade vulnerability search strategy. Simulated annealing is an adaptation of the simulation of physical thermodynamic annealing principles described by [11] to the minimisation of combinatorial optimisation problems [12] [13]. In common with genetic algorithms [14] and tabu search techniques [15] it follows the "local improvement" paradigm for harnessing the exponential complexity of the solution space.
The algorithm is based on randomisation techniques. An overview of algorithms based on such techniques can be found in [16]. A complete presentation of the method and its applications can be found in [17] and accessible algorithms for its implementation are presented by [18].
Simulated annealing is an optimisation
method suitable for combinatorial minimisation problems such as
the cascade vulnerability problem. Such problems exhibit a discrete,
factorially large configuration space. In common with all paradigms
based on "local improvements" the simulated annealing
method starts with a non-optimal initial configuration (which
may be chosen at random) and works on improving it by selecting
a new configuration using a suitable mechanism (at random in the
simulated annealing case) and calculating the corresponding cost
differential (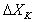 ). If the cost is reduced,
then the new configuration is accepted and the process repeats
until a termination criterion is satisfied. Unfortunately, such
methods can become "trapped" in a local optimum that
is far from the global optimum. Simulated annealing avoids this
problem by allowing "uphill" moves based on a model
of the annealing process in the physical world.
). If the cost is reduced,
then the new configuration is accepted and the process repeats
until a termination criterion is satisfied. Unfortunately, such
methods can become "trapped" in a local optimum that
is far from the global optimum. Simulated annealing avoids this
problem by allowing "uphill" moves based on a model
of the annealing process in the physical world.
When metals slowly cool and anneal, their atoms are often ordered in the minimal energy crystalline state for distances billions of times their diameter in all directions i.e., the solid is in a state of a global minimum. During the cooling process the system can escape local minima by moving to a thermal equilibrium of a higher energy potential based on the probabilistic distribution w of entropy S
where k is Boltzmann's constant and w the probability that the system will exist in the state it is in relative to all possible states it could be in. Thus given entropy's relation to energy E and temperature T
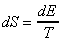
we arrive at the probabilistic expression w of energy distribution for a temperature T

This so-called Boltzmann probability distribution is illustrated in Figure 4. The probabilistic "uphill" energy movement that is made possible avoids the entrapment of local minima and can provide a globally optimal solution.
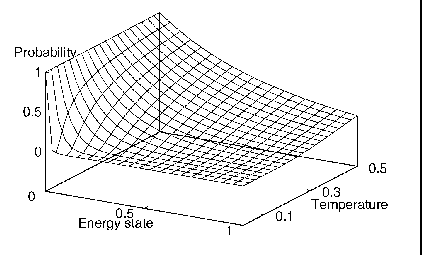
Figure 4: Probability distribution
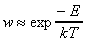 of energy states according to temperature.
of energy states according to temperature.
The application of the annealing
optimisation method to other processes works by repeatedly changing
the problem configuration and gradually lowering the temperature
until a minimum is reached. Our proposed solution is based on
Fitch's shortest path formulation modified to take into account
the simulated annealing search method. An outline of the algorithm's
pseudocode is as follows:
select a path P0 and an initial temperature T0;
repeat until no more vulnerable paths can be found:
repeat for a number of optimisation steps for the given temperature:
select a new path Pn by
moving a random amount of path segments
from one randomly selected position to another;
calculate the energy differential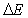 between
the current path C and the new one Pn;
between
the current path C and the new one Pn;
If the new path Pn
is more vulnerable ( ) or
) or
it satisfies the Metropolis criterion: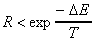 for
a random number R, 0 < R < 1
for
a random number R, 0 < R < 1
and an annealing temperature T then
make the new path Pn the current path C;
lower the annealing temperature
T following the cooling schedule.
After the simulated annealing optimisation
step is performed our proposed approach, similarly with Fitch's
approach, analyses the shortest path results to determine the
network security metric and accordingly adjusts the network or
the participating entities.
5. Conclusions
A network of computers is exposed to the Cascade Vulnerability problem when data of a security level d can be passed to a user with a lower security clearance u elsewhere on the network, without having to defeat any single component of the system that has an accreditation range great enough to allow users of level u and data of level d on a single system.
Many algorithms have been proposed
in the literature to deal with the cascade vulnerability detection.
In the previous sections we reviewed the basic properties of the
most important algorithms, conducted a brief comparative analysis
of them, and explained why the cascade vulnerability correction
problem is NP-complete. Our proposed solution based on the simulated
annealing approach provides a more efficient search strategy.
Possible future work involves the evaluation of this strategy
on existing problems and the adjustment of the simulated annealing
algorithm operating parameters.
6. References
7. Biographies
Stefanos Gritzalis
holds a BSc in Physics and an MSc in Electronic Automation, both
from the University of Athens, Greece. He is also pursuing a PhD
degree on Distributed Systems Security, with the Department of
Informatics of the University of Athens, Greece. Currently, he
is an Assistant Professor with the Department of Informatics of
the Technological Educational Institute (TEI) of Athens, Greece.
He has been involved in several national and EU funded R&D
projects in the areas of Computer Security, and Distributed Systems.
He is the author of more than 10 technical papers and conference
presentations. His research interests include Distributed Systems,
Computer Systems Security, and Operating Systems.
Diomidis Spinellis
holds an MEng in Software Engineering and a PhD in Computer Science
both from Imperial College (University of London). Currently he
is lecturing at the University of the Aegean, Greece. He has provided
consulting services to a number of Greek and international Information
Technology companies and has been involved in several national
and EU funded R&D projects in the areas of Computer Security,
Language Engineering, and Scientific Visualisation. He is the
author of more than 25 technical papers and conference presentations.
He has contributed software to the 4.4BSD Unix distribution, the
X-Windows system, he is the author of a number of public domain
software packages, libraries, and tools, and is a four times winner
of the International Obfuscated C Code Contest. His research interests
include Information Security, Software Engineering, and Programming
Languages.