![[line] An N-workstation multi-machine production line with N-1 intermediate buffers](figure1.png)
[line] An \(N\)-workstation multi-machine production line with \(N-1\) intermediate buffers
|
http://www.dmst.aueb.gr/dds/pubs/jrnl/1999-IJPR-Optim/html/bap.html This is an HTML rendering of a working paper draft that led to a publication. The publication should always be cited in preference to this draft using the following reference:
|
Large production line optimisation using simulated annealing4
Keywords: Buffer Allocation, Non-linear, Stochastic, Integer, Network Design, Simulated Annealing
A large amount of research has been devoted to the analysis and design of production lines. A lot of this research concerns the design of manufacturing systems with considerable inherent variability in the processing times at the various stations, a common situation with human operators/assemblers. The literature on the modelling and optimisation of production lines is vast, allowing us to review only the most directly relevant studies. For a systematic classification of the relevant works on the stochastic modelling of these and other types of manufacturing systems (e.g., transfer lines, flexible manufacturing systems (FMS), and flexible assembly systems (FAS)), the interested reader is referred to a review paper by Papadopoulos and Heavey (1996) and some recently published books, such as those by Askin and Standridge (1993), Buzacott and Shanthikumar (1993), Gershwin (1994), Papadopoulos et al. (1993), Viswanadham and Narahari (1992), and Altiok (1997). There are two basic problem classes:
the evaluation of production line performance measures such as throughput, mean flow time, workstation mean queue length, and system utilisation, and
the optimisation of the decision variables of these lines.
Examples of decision variables that have been considered are:
the sizes of the buffers placed between successive workstations of the lines,
the number of servers allocated to each workstation, and
the amount of workload allocated to each workstation.
The corresponding optimisation problems are named, respectively, (1) the buffer allocation problem, (2) the server allocation problem, and (3) the workload allocation problem, in a production line.
In Papadopoulos et al. (1993) both evaluative and generative (optimisation) models are given for modelling the various types of manufacturing systems. This work falls into the second category. Evaluative and optimisation models can be combined by closing the loop between them; that is, one can use feedback from an evaluative model to modify the decisions taken by the optimisation model.
One of the key questions that the designers face in a serial production line is the buffer allocation problem (BAP), i.e., how much buffer storage to allow and where to place it within the line. This is an important question because buffers can have a great impact on the efficiency of the production line. They compensate for the blocking and the starving of the line’s stations. For this reason, the buffer allocation problem has received a lot more attention than the other two design problems. Buffer storage is expensive due both to its direct cost, and to the increase of the work-in-process (WIP) inventories. In addition, the requirement to limit the buffer storage can also be a result of space limitations in the shop floor. The literature on the BAP is extensive. A systematic classification of the research work in this area is given in Singh and MacGregor Smith (1997) and Papadopoulos et al. (1993). The works are split according to:
search methods, Altiok and Stidham (1983), Smith and Daskalaki (1988), Seong, Chang, and Hong (1995), F. S. Hillier and So (1991a), F. S. Hillier and So (1991b), dynamic programming methods, Kubat and Sumita (1985), Jafari and Shanthikumar (1989), Yamashita and Altiok (1997), among others, and simulation methods, Conway et al. (1988), Ho, Eyler, and Chien (1979).
balanced/unbalanced, (Powell (1994) presents a literature review according to this scheme), or reliable/unreliable; the majority of papers deal with reliable lines. Only a few algorithms have been developed to calculate the performance measures of unreliable production lines Glassey and Hong (1983), Choong and Gershwin (1987), Gershwin (1989), Heavey, Papadopoulos, and Browne (1993). Hillier and So (1991a) and Seong, Chang, and Hong (1995) have dealt with the buffer allocation problem in unreliable production lines.
Similarly, few researchers have dealt with the buffer allocation problem in production lines with multiple (parallel) machines at each workstation Hillier and So (1995), Magazine and Stecke (1996), Singh and Smith (1997).
Apart from the buffer allocation problem, the other two interesting design problems have also been considered by some researchers, e.g., the work allocation problem Hillier and Boling (1979), Hillier and Boling (1966), Hillier and Boling (1977), Ding and Greenberg (1991), Huang and Weiss (1990), Shanthikumar, Yamazaki, and Sakasegawa (1991), Wan and Wolff (1993), Yamazaki, Sakasegawa, and Shanthikumar (1992), among others, and the server allocation problem Magazine and Stecke (1996), Hillier and So (1989). Hillier and So (1995) studied various combinations of these three design problems. Other references may be found therein Buzacott and Shanthikumar (1992), Buzacott and Shanthikumar (1993), among others.
The present work deals with the same design problems (buffer allocation, server allocation, and workload allocation) but for long production lines with multi-machine stations.
As the problem being investigated is combinatorial in nature, traditional Operations Research techniques are not as practical for obtaining optimal solutions for long production lines. We propose a simulated annealing (SA) approach as the search method in conjunction with the expansion method developed by Kerbache and MacGregor Smith (1987) as the evaluative tool. Simulated annealing is an adaptation of the simulation of physical thermodynamic annealing principles described by Metropolis et al. (1953) to the combinatorial optimisation problems Kirkpatrick, Gelatt Jr., and Vecchi (1983), Cerny (1985). Similar to genetic algorithms Holland (1975), Goldberg (1989) and tabu search techniques Glover (1990) it follows the ‘local improvement’ paradigm for harnessing the exponential complexity of the solution space.
The algorithm is based on randomisation techniques. An overview of algorithms based on such techniques can be found in the survey by Gupta et al. (1994). A complete presentation of the method and its applications is described by Van Laarhoven and Aarts (1987) and accessible algorithms for its implementation are presented by Corana et al. (1987) and Press et al. (1988). A critical evaluation of different approaches to annealing schedules and other method optimisations are given by Ingber (1993). As a tool for operational research SA is presented by Eglese (1990), while Koulamas et al. (1994) provide a complete survey of SA applications to operations research problems.
The use of the Simulated Annealing algorithm appears to be a promising approach. We believe that this algorithm could be applied in conjunction with a fast decomposition algorithm to solve efficiently and accurately the aforementioned optimisation problems in much longer production lines.
The remainder of the paper is organised as follows: we first describe the production line model and the problem of our interest followed by the methodology of our approach namely: the performance model, the expansion method used for evaluating the line performance, an overview of the combinatorial optimisation methods, the simulated annealing optimisation method, and the complete enumeration method; we then describe our experimental methodology and present an overview of the numerical and performance results for short and long production lines. In the Appendix following the concluding section, we provide a full tabulated set of the experimental results.
We define an asynchronous line as one in which every workstation can pass parts on when its processing is complete as long as buffer space is available. Such a line is subject to manufacturing starving and blocking. We assume that the first station is never starved and the last station is never blocked. Therefore we can say that the line operates in a push mode: parts are always available when needed at the first workstation and space is always available at the last workstation to dispose of completed parts.
![[line] An N-workstation multi-machine production line with N-1 intermediate buffers](figure1.png)
[line] An \(N\)-workstation multi-machine production line with \(N-1\) intermediate buffers
An \(N\)-station line consists of \(N\) workstations in series, labelled \(M_{1}, M_{2}, \ldots, M_{N}\) and \(N-1\) locations for buffers, labelled \(B_{2}, B_{3}, \ldots, B_{N}\), is illustrated in figure [line]. Each station \(i\) has \(s_{i}\) servers operating in parallel. The buffer capacities of the intermediate buffers \(B_{i}\), \(i=2,\ldots,N\), are denoted by \(q_{i}\), whereas the mean service times of the \(i\) stations (\(i=1,\ldots,N\)) are denoted by \(w_{i}\).
The main performance measure of the production line is the mean throughput, denoted by \(R(\underline{q},\underline{s},\underline{w})\), where \(\underline{q}\)\(=(q_{2},q_{3},\ldots,q_{N})\), \(\underline{s}\)\(=(s_{1},s_{2},\ldots,s_{N})\) and \(\underline{w}\)\(=(w_{1},w_{2},\ldots,w_{N})\).
If \(Q\) denotes the total number of available buffer slots to be allocated to the \(N-1\) buffers and \(S\) the total number of available servers (machines) to allocated to the \(N\) stations then the general version of the optimisation model (first reported by Hillier and So, 1995) is:
\[\max R(\underline{q},\underline{s},\underline{w}) \label{1}\]
subject to:
\[\begin{aligned} \sum_{i=2}^{N} q_{i} = Q, \label{2} \\ \sum_{i=1}^{N} s_{i} = S, \label{3} \\ \sum_{i=1}^{N} w_{i} = N, \label{4}\end{aligned}\]
\[q_{i} \geq 0 \wedge \mathrm{integer} (i=2,3,\ldots,N),\] \[s_{i} \geq 1 \wedge \mathrm{integer} (i=1,2,\ldots,N),\] \[w_{i} > 0 (i=1,2,\ldots,N),\] where \(Q,S\) and \(N\) are fixed constants and \(\underline{q}\), \(\underline{s}\) and \(\underline{w}\) are the decision vectors. The third constraint indicates that the sum of the expected service times is a fixed constant, which by normalisation can be equal to \(N\).
The objective function of throughput, \(R(\underline{q},\underline{s},\underline{w})\), is not the only performance measure of interest. The average WIP, the flow time, the cycle time, the system utilisation, the average queue lengths and other measures are equally important performance measures. However, throughput is the most commonly used performance measure in the international literature.
The queuing model \(M/M/C/K\) that we use refers to a queuing system where:
it is assumed that the arrivals are distributed according to the Poisson distribution (or equivalently that the intermediate times between two successive arrivals are exponentially distributed),
the service (processing) times follow the exponential distribution,
there are \(C\) parallel servers (machines which are identical at each workstation), and
the total capacity of the system is finite and equal to \(K\).
While our focus in this paper is on \(M/M/C/K\) approximations for open queuing networks of series-parallel topologies, we also briefly discuss some of the available approaches used for modelling \(M/M/1/K\) systems since most of the literature has focused on \(M/M/1/K\) systems.
Both open and closed systems have been studied by exact analysis although results have been limited. Exact analyses of open two, three, and four node-server models with exponential service are limited by the explosive growth of the Markov chain models for analysing these systems. The analysis of very large Markov chain models has led to effective aggregation techniques for these models Schweitzer and Altiok (1989), Takahashi (1989) but the computation time and power required for these exact results leaves open the need for approximation techniques.
Van Dijk and his co-authors (1988; 1989) have developed some bounding methodologies for both \(M/M/1/K\) and \(M/M/C/K\) systems and have demonstrated their usefulness in the design of small queuing networks. Of course, when doing optimisation of medium and long queuing networks, bounds can be far off the optimum, so robust approximation techniques close to the optimal performance measures are most desirable.
Most approximation techniques appearing in the literature rely on decomposition/aggregation methods to approximate performance measures. One and two node decompositions of the network have been carried out, all with varying degree of success.
The few approximation approaches available in the literature can be classified as follows: Isolation methods, Repeated Trials, Node-by-node decomposition, and Expansion methods. In the Isolation method, the network is subdivided into smaller subnetworks and then studied in isolation Labetoulle and Pujolle (1980), Boxma and Konheim (1981). This method was used by Kuehn (1979) and Gelenbe and Pujolle (1976) but they failed to consider networks with finite capacity.
Closely related to the Isolation method is the Repeated Trials Method, a class of techniques based upon repeatedly attempting to send blocked customers to a queue causing the blocking Caseau and Pujolle (1979), Fredericks and Reisner (1979), Fredericks (1980).
In Node-by-node decomposition, the network is broken down into single, pairs, and triplets of nodes with augmented service and arrival parameters which are then studied separately Hillier and Boling (1967), Takahashi, Miyahara, and Hasegawa (1980), Altiok (1982), Altiok and Perros (1986), Perros and Altiok (1986), Brandwajn and Jow (1988). More general service time approximations appear in the work by Gun and Makowski (1989). The Expansion method is the approach argued for in this paper for computing the performance measures of \(M/M/C/K\) finite queuing networks Kerbache (1984), Kerbache and Smith (1987), Kerbache and Smith (1988). It can be characterised conceptually as a combination of Repeated Trials and Node-by-Node Decomposition where the key difference is that a ‘holding’ node is added to the network to register blocked customers. The addition of the holding node ‘expands’ the network. This approach transforms the queuing network into an equivalent Jackson network which is then decomposed allowing for each node to be solved independently. We have successfully used the Expansion Method to model \(M/M/1/K\) Kerbache and Smith (1988), \(M/M/C/K\) Jain and Smith (1994), Han and Smith (1992), \(M/G/1/K\) Kerbache and Smith (1987), and most recently \(M/G/C/C\) Cheah and Smith (1994), Smith (1991), Smith (1994) queues and queuing networks. In addition, we have also used our Expansion Methodology to model routing Daskalaki and Smith (1989), Daskalaki and Smith (1986), Gosavi and Smith (1990) and optimal resource allocation problems Smith and Daskalaki (1988), Smith (1991), Smith and Chikhale (1995), Singh and Smith (1997).
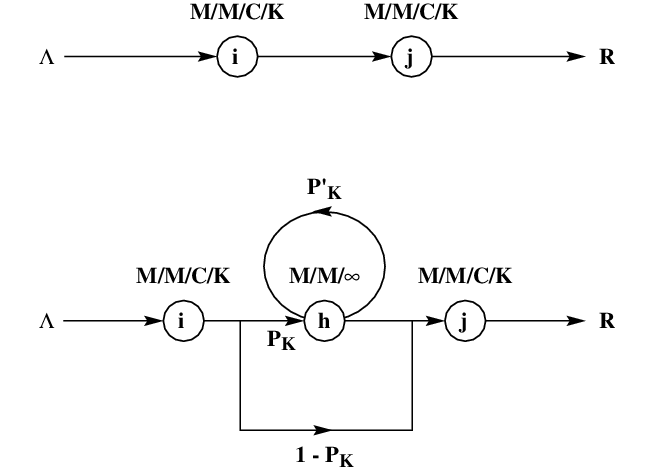
The Expansion Method is a robust and effective approximation technique developed by Kerbache and Smith (1987). As described in previous papers, this method is characterised as a combination of Repeated Trials and Node-by-node Decomposition solution procedures. Methodologies for computing performance measures for a finite queuing network use primarily the following two kinds of blocking:
The upstream node \(i\) gets blocked if the service on a customer is completed but it cannot move downstream due to the queue at the downstream node \(j\) being full. This is sometimes referred to as Blocking After Service (BAS) Onvural (1990).
The upstream node is blocked when the downstream node becomes saturated and service must be suspended on the upstream customer regardless of whether service is completed or not. This is sometimes referred to as Blocking Before Service (BBS) Onvural (1990).
The Expansion Method uses Type I blocking, which is prevalent in most production and manufacturing, transportation and other similar systems.
Consider a single node with finite capacity \(K\) (including service). This node essentially oscillates between two states — the saturated phase and the unsaturated phase. In the unsaturated phase, node \(j\) has at most \( K- 1 \) customers (in service or in the queue). On the other hand, when the node is saturated no more customers can join the queue. Refer to figure [Blocking] for a graphical representation of the two scenarios.
Type I Blocking in Finite Queues
The Expansion Method consists of the following three stages :
Stage I: Network Reconfiguration.
Stage II: Parameter Estimation.
Stage III: Feedback Elimination.
The following notation defined by Kerbache and Smith (1987; 1988) shall be used in further discussion regarding this methodology :
\( h:=\) The holding node established in the Expansion method.
\(\Lambda \) := External Poisson arrival rate to the network.
\( \lambda_{j} \) := Poisson arrival rate to node \(j\).
\(\tilde{\lambda_{j}}\):= Effective arrival rate to node \(j\).
\( \mu_{j}\) := Exponential mean service rate at node \( j \).
\(\tilde{\mu_{j}}\) := Effective service rate at node \( j \) due to blocking.
\( p_{K}\):= Blocking probability of finite queue of size \(K\).
\( p_{K}'\):=Feedback blocking probability in the Expansion method.
\( p_{0}^{j}\) :=Unconditional probability that there is no customer in the service channel at node \( j \) (either being served or being held after service).
\(R \) := Mean throughput rate.
\( S_{j}\) := Service capacity (buffer) at node \(j\), i.e. \( S= K \) for a single queue.
Using the concept of two phases at node \(j\), an artificial node \(h\) is added for each finite node in the network to register blocked customers. Figure [Blocking] shows the additional delay, caused to customers trying to join the queue at node \(j\) when it is full, with probability \(p_{K}\). The customers successfully join queue \(j\) with a probability \((1 - p_{K})\). Introduction of an artificial node also dictates the addition of new arcs with \(p_{K}\) and \((1 - p_{K})\) as the routing probabilities.
The blocked customer proceeds to the finite queue with probability \((1- p_{K}')\) once again after incurring a delay at the artificial node. If the queue is still full, it is re-routed with probability \( p_{K}'\) to the artificial node where it incurs another delay. This process continues till it finds a space in the finite queue. A feedback arc is used to model the repeated delays. The artificial node is modelled as an \(M/M/\infty\) queue. The infinite number of servers is used simply to serve the blocked customer a delay time without queuing.
This stage essentially estimates the parameters \(p_{K}\), \(p_{K}'\) and \(\mu_{h}\) utilising known results for the \(M/M/C/K\) model.
\(p_{K}\) : Analytical results from the \(M/M/C/K\) model provide the following expression for \(p_{K}\):
\[p_{K} = {{1}\over{c^{K-c} c!}} {\left(\frac{\lambda}{\mu}\right)}^{K} p_{0}\]
where for \((\lambda/c\mu \not = 1)\)
\[p_{0}= \left[ \sum^{c-1}_{n=0} \frac{1}{n!} \left( {\frac{\lambda}{\mu}}\right)^{n} + \frac{(\lambda/\mu)^{c}}{c!} \frac{1 - (\lambda/c\mu)^{K-c+1}}{1 - \lambda/c\mu} \right]^{-1}\]
and for \((\lambda/c\mu = 1)\),
\[p_{0} = \left[\sum_{n=0}^{c-1} \frac{1}{n!} \left(\frac{\lambda}{\mu}\right)^{n} + \frac{(\lambda/\mu)^{c}}{c!}(K- c + 1) \right]^{-1}\]
\(p_{K}'\): Since there is no closed form solution for this quantity an approximation is used given by Labetoulle and Pujolle obtained using diffusion techniques Labetoulle and Pujolle (1980).
\[p_{K}' = \left[\frac{\mu_{j} + \mu_{h}}{\mu_{h}} - \frac{\lambda [(r_{2}^{K} - r_{1}^{K}) - (r_{2}^{K-1} - r_{1}^{K-1})]} {\mu_{h}[(r_{2}^{K+1} - r_{1}^{K+1}) - (r_{2}^{K} - r_{1}^{K})]}\right]^{-1}\]
where \(r_{1}\) and \(r_{2}\) are the roots to the polynomial:
\[\lambda - (\lambda + \mu_{h} + \mu_{j})x + \mu_{h}x^{2} = 0\]
while, \(\lambda = \lambda_{j} - \lambda_{h}(1 - p_{K}')\) and \(\lambda_{j}\) and \(\lambda_{h}\) are the actual arrival rates to the finite and artificial holding nodes respectively.
In fact, \(\lambda_{j}\) the arrival rate to the finite node is given by: \[\lambda_{j} = \tilde{\lambda_{i}}(1 - p_{K}) = \tilde{\lambda_{i}} - \lambda_{h}\]
Let us examine the following argument to determine the service time at the artificial node. If an arriving customer is blocked, the queue is full and thus a customer is being serviced, so the arriving customer to the holding node has to remain in service at the artificial holding node for the remaining service time interval of the customer in service. The delay distribution of a blocked customer at the holding node has the same distribution as the remaining service time of the customer being serviced at the node doing the blocking. Using renewal theory, one can show that the remaining service time distribution has the following rate \(\mu_h\):
\[\mu_{h} = \frac{2\mu_{j}}{1 + \sigma^{2}\mu_{j}^{2}}\]
where, \(\sigma^{2}\) is the service time variance given by Kleinrock (1975). Notice that if the service time distribution at the finite queue doing the blocking is exponential with rate \(\mu_j\), then: \[\mu_{h} = \mu_j\] the service time at the artificial node is also exponentially distributed with rate \(\mu_j\).
Due to the feedback loop around the holding node, there are strong dependencies in the arrival processes. Elimination of these dependencies requires reconfiguration of the holding node which is accomplished by recomputing the service time at the node and removing the feedback arc. The new service rate is given by:
\[\mu_{h}' = (1 - p_{K}')\mu_{h}\]
The probabilities of being in any of the two phases (saturated or unsaturated) are \(p_{K}\) and \( (1 - p_{K}) \). The mean service time at a node i preceding the finite node is \(\mu_{i}^{-1}\) when in the unsaturated phase and \((\mu_{i}^{-1} + \mu_{h}'^{-1}) \) in the saturated phase. Thus, on an average, the mean service time at the node i preceding a finite node is given by:
\[\tilde{\mu_{i}^{-1}} = \mu_{i}^{-1} + p_{K}\mu_{h}'^{-1}\]
Similar equations can be established with respect to each of the finite nodes. Ultimately, we have simultaneous non-linear equations in variables \(p_{K}\), \(p_{K}'\), \(\mu_{h}^{-1}\) along with auxiliary variables such as \(\mu_{j}\) and \( \tilde{\lambda_{i}} \). Solving these equations simultaneously we can compute all the performance measures of the network.
\[\begin{aligned} \lambda & = & \lambda_{j} - \lambda_{h}(1 - p_{K}') \label{exp:first} \\ \lambda_{j} & = & \tilde{\lambda_{i}}(1 - p_{K}) \label{exp:second} \\ \lambda_{j} & = & \tilde{\lambda_{i}} - \lambda_{h} \label{exp:third} \\ p_{K}' & = & \left[\frac{\mu_{j} + \mu_{h}}{\mu_{h}} - \frac{\lambda[(r_{2}^{K} - r_{1}^{K}) - (r_{2}^{K-1} - r_{1}^{K-1})]} {\mu_{h}[(r_{2}^{K+1} - r_{1}^{K+1}) - (r_{2}^{K} - r_{1}^{K})]}\right]^{-1} \label{exp:fourth} \\ z & = & (\lambda + 2\mu_{h})^{2} - 4\lambda\mu_{h} \label{exp:fifth}\\ r_{1} & = & \frac{[(\lambda + 2 \mu_{h}) - z^{\frac{1}{2}}]}{2\mu_{h}} \label{exp:sixth} \\ r_{2} & = & \frac{[(\lambda + 2 \mu_{h}) + z^{\frac{1}{2}}]}{2\mu_{h}} \label{exp:seventh} \\ p_{K} & = & \frac{1}{c^{K-c} c!} {\left(\frac{\lambda}{\mu}\right)}^{K} p_{0} \label{exp:eigth} \end{aligned}\]
Equations [exp:first] to [exp:fourth] are related to the arrivals and feedback in the holding node. The equations [exp:fifth] to [exp:seventh] are used for solving equation [exp:fourth] with \(z\) used as a dummy parameter for simplicity of the solution. Lastly, equation [exp:eigth] gives the approximation to the blocking probability derived from the exact model for the \(M/M/C/K\) queue. Hence, we essentially have five equations to solve, viz. [exp:first] to [exp:fourth] and [exp:eigth]. To recapitulate, we first expand the network with an artificial holding node; this stage is then followed by the approximation of the routing probabilities, due to blocking, and the service delay in the holding node; and, finally, the feedback arc at the holding node is eliminated. Once these three stages are complete, we have an expanded network which can then be used to compute the performance measures for the original network. As a decomposition technique this approach allows successive addition of a holding node for every finite node, estimation of the parameters and subsequent elimination of the holding node.
The Buffer Allocation Problem (BAP) is perhaps best formulated as a non-linear multiple-objective programming problem where the decision variables are the integers. Not only is the BAP a difficult \(\cal NP-\)hard combinatorial optimisation problem, it is made all the more difficult by the fact that the objective function is not obtainable in closed form to interrelate the integer decision variables \(\bar x\) and the performance measures such as throughput \(R\), work-in-process \(\bar L\), total buffers allocated \(\sum_ix_i\), and other system performance measures such as system utilisation \(\bar \rho\) for any but the most trivial situations. Combinatorial Optimisation approaches for solving problems like the BAP are generally classified as either exact optimal approaches or heuristic ones.
Exact approaches are appropriate for solving small problem instances or for problems with special structure e.g. the Travelling Salesman Problem, which admit optimal solutions. Classical approaches for achieving an optimal solution include Branch-and-Bound, Branch-and-Cut, Dynamic Programming, Exhaustive Search, and related implicit and explicit enumeration methods. The difficulty with utilising these exact approaches for the BAP such as Branch-and-Bound is that the subproblems for which one seeks to compute upper and lower bounds on the objective function are stochastic, non-linear programming problems which are as difficult as the original problem so little is gained by these exact problem decomposition methods.
This dilemma implies that heuristic approaches are the only reasonable methodology for large scale problem instances of the BAP problem. Heuristic approaches can be classified as either classical Non-linear Programming search methods or Metaheuristics.
Non-linear Programming (derivative-free) search Himmelblau (1972) methods such as, to name a few, Hooke-Jeeves, Nelder-Mead simplex methods, PARTAN, Powell’s Conjugate Direction metods, Flexible Tolerance, the Complex Method of Box, and other related techniques have met with varied levels of success in the BAP literature and are viable means of dealing with the BAP because of the non-closed form nature of the non-linear objective function. While many researchers feel that the objective function is concave or pseudo-concave in the decision variables, the discrete nature of the decision variables makes the problem discontinuous and so no derivative information is available.
Metaheuristic methods such as Simulated Annealing, Tabu Search, Genetic Algorithms, and related techniques have not historically been utilised to solve the BAP; in this paper we shall explore the use of Simulated Annealing.
Simulated annealing is an optimisation method suitable for combinatorial optimisation problems. Such problems exhibit a discrete, factorially large configuration space. In common with all paradigms based on ‘local improvements’ the simulated annealing method starts with a non-optimal initial configuration (which may be chosen at random) and works on improving it by selecting a new configuration using a suitable mechanism (at random in the simulated annealing case) and calculating the corresponding cost differential (\(\Delta R_{K}\)). If the cost is reduced, then the new configuration is accepted and the process repeats until a termination criterion is satisfied. Unfortunately, such methods can become ‘trapped’ in a local optimum that is far from the global optimum. Simulated annealing avoids this problem by allowing ‘uphill’ moves based on a model of the annealing process in the physical world.
![[boltzmann] Probability distribution w \sim \exp(\frac{-E}{kT}) of energy states according to temperature.](figure3.png)
[boltzmann] Probability distribution \(w \sim \exp(\frac{-E}{kT})\) of energy states according to temperature.
Physical matter can be brought into a low-temperature ground state by careful annealing. First the substance is melted, then it is gradually cooled with a lot of time spent at temperatures near the freezing point. If this procedure is not followed the resulting substance may form a glass with not crystalline order and only metastable, consisting of locally optimal structures Kirkpatrick, Gelatt Jr., and Vecchi (1983). During the cooling process the system can escape local minima by moving to a thermal equilibrium of a higher energy potential based on the probabilistic distribution \(w\) of entropy \(S\): \[% Halliday & Resnick (25-15) p. 557 S = k \ln w\] where \(k\) is Boltzmann’s constant and \(w\) the probability that the system will exist in the state it is in relative to all possible states it could be in. Thus given entropy’s relation to energy \(E\) and temperature \(T\): \[% Halliday & Resnick (25-9) p. 552 dS = \frac{d\bar{ }E}{T}\] we arrive at the probabilistic expression \(w\) of energy distribution for a temperature \(T\): \[w \sim \exp(\frac{-E}{kT})\] This so-called Boltzmann probability distribution is illustrated in figure [boltzmann]. The probabilistic ‘uphill’ energy movement that is made possible avoids the entrapment in a local minimum and can provide a globally optimal solution.
The application of the annealing optimisation method to other processes works by repeatedly changing the problem configuration and gradually lowering the temperature until a minimum is reached.
The correspondence between annealing in the physical world and simulated annealing as used for production line optimisation is outlined in table [corr].
| Physical World | Production Line Optimisation |
|---|---|
| Atom placement | Line configuration |
| Random atom movements | Buffer space, server, service rate movement |
| Energy \(E\) | Throughput \(R\) |
| Energy differential \(\Delta E\) | Configuration throughput differential \(\Delta R\) |
| Energy state probability distribution | Changes according to the Metropolis criterion, \(\exp(\frac{-\Delta E}{T}) > \mathrm{rand} (0 \ldots 1)\), implementing the Boltzmann probability distribution |
| Temperature | Variable for establishing configuration acceptance termination |
As a base-rate benchmark for our approach, we used complete enumeration (CE) of all possible buffer and server allocation possibilities. The number of feasible allocations of \(Q\) buffer slots among the \(N-1\) intermediate buffer locations and \(S\) servers among the \(N\) stations increases dramatically with \(Q\), \(S\), and \(N\) and is given by the formula: \[\label{cenum} \begin{array}{l} \left( \begin{array}{c} Q + N - 2 \\ N - 2 \end{array} \right) \left( \begin{array}{c} S + N - 1 \\ N - 1 \end{array} \right) = \\ \frac{(Q+1)(Q+2)\cdots(Q+N-2)} {(N-2)!} \frac{(S+1)(S+2)\cdots(S+N-1)} {(N-1)!} \end{array}\]
All buffer and server combinations can be methodically enumerated by considering a vector \(\underline{p}\) denoting the position within the production line of each buffer or server. Given the vector \(\underline{p}\) we can then easily map \(\underline{p}\) to \(\underline{q}\) or \(\underline{s}\) using the following equation (for the case of \(\underline{q}\)): \[q_{i} = \sum_{j=1}^{Q} \left\{ \begin{array}{ll} 1 & \mathrm{if}\ p_{j} = i \\ 0 & \mathrm{otherwise} \end{array} \right.\] Given then a buffer or server configuration \(\underline{p}\) we advance to the next configuration \(\underline{p}'\) using the function g: \[\underline{p}' = \mathrm{g}(\underline{p}, 1)\] where g is recursively defined (for \(Q\) buffers) as: \[\mathrm{g}(\underline{p}, l) = \left\{ \begin{array}{ll} \begin{array}{l} (p_{1}, \ldots, p_{l}+1, \ldots, p_{Q}) \end{array} & \mathrm{if}\ p_{l} + 1 \leq N \\ \begin{array}{l} (p'_{1}, \ldots, p'_{l-1}, p'_{l+1}, \ldots, p'_{l+1}) \\ \mathrm{where}\ \underline{p}' = \mathrm{g}(\underline{p}, l + 1) \end{array} & \mathrm{otherwise} \end{array} \right.\] Essentially, g maps the vector of positions to a new one representing another line configuration. When the position \(p_{i}\) of buffer or server resource \(i\), as it is incremented, reaches the last place in the line \(N\) (\(p_{i} + 1 = N\)) g is recursively applied to the buffer or server in position \(p_{i+1}\) setting \(p_{i}\)–\(p_{Q}\) to the new value of \(p_{i+1}\). The complete enumeration terminates when all buffers or servers reach the line position \(N\). To enumerate all buffer and server combinations one complete server enumeration is performed for each line buffer configuration.
The main generative procedure we used was Simulated Annealing Kirkpatrick, Gelatt Jr., and Vecchi (1983), Van Laarhoven and Aarts (1987), Spinellis and Papadopoulos (1997) with complete enumeration used where practical in order to validate the SA results. In order to test the approach, 339 cases of small and large production lines from a wide combination of allocation options were searched using SA or CE.
The generalised queuing network throughput evaluation algorithm was initially ported from a vax vms operating system, to a PC-based Intel architecture. Most changes involved the adjustment of numerical constants according to the ieee 488 floating point representation used on the Intel platforms. Subsequently, the algorithm was rewritten in a pure subroutine form so that it could be repeatedly called from within a program and semi-automatically converted from fortran to ansi c.
The SA algorithm used for the production line resource optimisation is given in the figure below.
\([\)Set initial line configuration.\(]\) Set \(q_{i} \leftarrow \lfloor Q/N \rfloor\), set \(q_{N/2} \leftarrow q_{N/2} + Q - \sum_{i=2}^{N} \lfloor Q/N \rfloor\), set \(s_{i} \leftarrow \lfloor S/N \rfloor\), set \(s_{N/2} \leftarrow s_{N/2} + S - \sum_{i=1}^{N} \lfloor S/N \rfloor\), set \(w_{i} \leftarrow 1/N\).
\([\)Set initial temperature \(T_{0}\).\(]\) Set \(T \leftarrow 0.5\).
\([\)Initialize step and success count.\(]\) Set \(S \leftarrow 0\), set \(U \leftarrow 0\).
\([\)Create new line with a random redistribution of buffer space, servers, or service rate.\(]\)
\([\)Create a copy of the configuration vectors.\(]\) Set \(\underline{q}' \leftarrow \underline{q}\), set \(\underline{s}' \leftarrow \underline{s}\), set \(\underline{w}' \leftarrow \underline{w}\).
\([\)Determine which vector to modify.\(]\) Set \(R_{v} \leftarrow \lfloor \mathrm{rand} [0 \ldots 2] \rfloor\).
if \(R_{v} = 0\) \([\)Create new line with a random redistribution of buffer space.\(]\) Move \(R_{n}\) space from a source buffer \(q_{R_{s}}\) to a destination buffer \(q_{R_{d}}\): set \(R_{s} \leftarrow \lfloor \mathrm{rand} [2 \ldots N)\rfloor\), set \(R_{d} \leftarrow \lfloor \mathrm{rand} [2 \ldots N)\rfloor\), set \(R_{n} \leftarrow \lfloor \mathrm{rand} [1 \ldots q_{R_{s}}+1)\rfloor\), set \(q_{R_{s}} \leftarrow q_{R_{s}} - R_{n}\), set \(q_{R_{d}} \leftarrow q_{R_{d}} + R_{n}\).
if \(R_{v} = 1\) \([\)Create new line with a random redistribution of server allocation.\(]\) Move \(R_{n}\) servers from source station \(s_{R_{s}}\) to a destination station \(s_{R_{d}}\): set \(R_{s} \leftarrow \lfloor \mathrm{rand} [1 \ldots N)\rfloor\), set \(R_{d} \leftarrow \lfloor \mathrm{rand} [1 \ldots N)\rfloor\), set \(R_{n} \leftarrow \lfloor \mathrm{rand} [1 \ldots s_{R_{s}}+1)\rfloor\), set \(s_{R_{s}} \leftarrow s_{R_{s}} - R_{n}\), set \(s_{R_{d}} \leftarrow s_{R_{d}} + R_{n}\).
if \(R_{v} = 2\) \([\)Create new line with a random redistribution of service rate.\(]\) Move \(R_{n}\) service rate from source station \(s_{R_{s}}\) to a destination station \(s_{R_{d}}\): set \(R_{s} \leftarrow \lfloor \mathrm{rand} [1 \ldots N)\rfloor\), set \(R_{d} \leftarrow \lfloor \mathrm{rand} [1 \ldots N)\rfloor\), set \(R_{n} \leftarrow \mathrm{rand} (0 \ldots w_{R_{s}}]\), set \(w_{R_{s}} \leftarrow w_{R_{s}} - R_{n}\), set \(w_{R_{d}} \leftarrow w_{R_{d}} + R_{n}\).
\([\)Calculate energy differential.\(]\) Set \(\Delta E \leftarrow R(\underline{q}, \underline{s}, \underline{w}) - R(\underline{q'}, \underline{s'}, \underline{w'})\).
\([\)Decide acceptance of new configuration.\(]\) Accept all new configurations that are more efficient and, following the Boltzmann probability distribution, some that are less efficient: if \(\Delta E < 0\) or \(\exp(\frac{-\Delta E}{T}) > \mathrm{rand} (0 \ldots 1)\), set \(\underline{q} \leftarrow \underline{q}'\), set \(\underline{s} \leftarrow \underline{s}'\), set \(\underline{w} \leftarrow \underline{w}'\), set \(U \leftarrow U + 1\).
\([\)Repeat for current temperature\(]\). Set \(S \leftarrow S + 1\). If \(S < \) maximum number of steps, go to step 4.
\([\)Lower the annealing temperature.\(]\) Set \(T \leftarrow c T\) (\(0 < c < 1\)).
\([\)Check if progress has been made.\(]\) If \(U > 0\), go to step 3; otherwise the algorithm terminates. \(\Box\)
The SA procedure was run with the following characteristics based on the number of stations \(N\):
\(100 \times N\)
\(10 \times N\)
\(0.5\)
Exponential: \(T_{K+1} = 0.9 T_{K}\)
Equal division of buffers and servers among stations with any remaining resources placed on the station in the middle.
Elapsed wall clock time in seconds.
The following facts clarify the use of the evaluation algorithm:
the throughput used as the line metric and presented in the tabulated results is the throughput at the last station,
the line topology graph is a linear series of stations allowing for parallel servers, and
the initial and the effective arrival rate at the first server are set to \(1.5\).
Three batches of tests were planned and executed. One, presented in tables [hr]–[hesb5], was planned in order to compare the results of our approach with those of Hillier and So (1995). A second set, presented in tables [b9]–[be15], was planned in order to compare the approach to the results obtained using a different evaluative procedure Spinellis and Papadopoulos (1997). Finally, the third batch of tests, presented in tables [b]–[bsr], aimed at establishing our method’s efficacy in determining optimal configurations of large production lines. Tables [b9]–[bsr] contain an additional column, \(T\), presenting the program execution time (\(s\)).
The following paragraphs outline the results we obtained by utilising the described methodology on a variety of problems. Where applicable we compare the obtained results with other published data. In our description of the results we sometimes refer to the phenomena of the bowl and the \(L\)-shape.
The bowl phenomenon occurs when for \(j=1,2,\ldots,N\), \[\begin{aligned} w_{j}^{*} & = & w_{N+1-j}^{*} \\ w_{j}^{*} & > & w_{j+1}^{*}~~~\left(1 \leq j \leq \frac{N-1}{2}\right) \\ w_{j}^{*} & < & w_{j+1}^{*}~~~\left(\frac{N-1}{2} \leq j \leq N+1\right)\end{aligned}\] The name arises from the fact that the value of \(w_{1}^{*}=w_{N}^{*}\) is considerably larger than the other \(w_{j}^{*}\), whereas the other \(w_{j}^{*}\) are relatively close, so that plotting the \(w_{j}^{*}\) versus \(j\) gives the shape of the cross-section of the interior of a bowl.
Correspondingly, the \(L\)-phenomenon is the allocation of extra servers to the first station of the production line. This leads to almost the maximum throughput of the line, which is attained when the extra servers are allocated to the last station of the line, having the advantage that it leads to less work-in-process inventory.
Tables [hr]–[hesb5] present results for the optimal allocation using SA for lines similar to the ones examined by Hillier and So (1995). In all cases CE results have been calculated for comparison purposes. In comparing the results obtained with those presented by Hillier and So the following important observations can be made:
The service rate allocation (table [hr]) does not follow the bowl phenomenon, but diminishes towards the end of the line.
The buffer allocation (table [hb]) does not follow the bowl phenomenon, but increases monotonically across the line.
The server allocation (table [hs]) for a small number of servers follows a pattern strikingly similar to the one presented in Hillier and So (1995). However, as the number of servers increases, servers tend to accumulate towards the beginning of the line.
The server and service rate allocation (table [hsr]) do not exhibit the \(L\)-phenomenon.
The buffer and service rate allocation (table [hbr]) results are very similar to the results presented in Hillier and So (1995). As far as the buffer allocation is concerned, buffers tend to accumulate towards the end of the line. The allocation of work however, does not exhibit the bowl phenomenon presented in the other study and follows the usual descending rate across the line.
The buffer and server allocation (tables [hsb34], [hsb5]) results are roughly similar to those presented in Hillier and So (1995) in both the server and the buffer allocation vectors. Servers tend to accumulate towards the beginning and middle of the line, whereas buffers tend to accumulate towards the line ends.
Finally, the buffer, server, and service rate allocation (table [hbrs]) roughly follows the shape of service rate allocation presented in Hillier and So (1995), but the allocation of buffers and servers is quite dissimilar.
Concerning the behaviour of SA compared to CE the results of the two methods are as follows:
Buffer allocation (tables [hb], [heb]) is the same using SA and CE.
The server allocation of a large number of servers (tables [hs], [hes]) using SA differs from the allocation using CE but only in the last two experiments, and this is probably due to incorrect results returned by the evaluation algorithm.
For buffer and server allocation for up to 4 stations (tables [hsb34], [hesb34]) SA and CE give the same results.
For buffer and server allocation of 5 stations (tables [hsb5], [hesb5]) SA and CE differ in the allocated vectors of some configurations, but with only a slight impact on the resulting throughput.
The tables ([b15]–[bsr]) present results for optimal allocation using SA for lines of \(N = 4-70\) stations with \(Q=2 N\) buffers and \(S=2 N\) servers. Where practical (i.e. for small lines) CE results have been calculated for comparison purposes. The optimal allocation of a variable number of buffers to a fixed number of servers (9 servers in table [b9]; 15 servers table [b15]) follows a regular pattern: buffers are added to the line from the right to the left. The results of the CE (table [be9]; table [be15]) confirm the SA results. However, this placement strategy is different from the optimal strategy obtained using the decomposition method Dallery and Frein (1993) as the evaluative procedure Spinellis and Papadopoulos (1997).
The execution time of the SA optimisation algorithm increased exponentially depending on the number of stations (figure [perf]). This increase was a lot better than the combinatorial explosion of CE, and allowed us to produce near-optimal configurations for relatively large production lines in reasonable time. At the extreme end for a 60 station line SA produced a solution for the allocation of 120 buffers, 120 servers, and the service rate configuration in \(4.5\) hours on a 120MHz Pentium-processor system. This solution using SA required the testing of 238,248 different configurations. The dominant factor of the algorithm is the line configuration evaluation taking on our system about 70ms for every configuration test. Multiplying this time factor by the number of all possible buffer and server allocation configurations for the above case — according to equation [cenum] — gives us an approximate evaluation time using CE of \( \left( \begin{array}{c} 120 + 60 - 2 \\ 60 - 2 \end{array} \right) \left( \begin{array}{c} 120 + 60 - 1 \\ 60 - 1 \end{array} \right) 0.07s = 10^{68}s\) or \(10^{62}\) years.
Our approach of using the expansion method for evaluating the production line configurations generated by simulated annealing optimisation allowed us to explore small and large line configurations in bounded execution time. The results obtained with our approach, compared to those of other studies exhibit some interesting similarities but also striking differences between them in the allocation of buffers, numbers of servers, and their service rates. While context dependent, these patterns of allocation are one of the most important insights which emerge in solving very long production lines. The patterns, however, are often counter-intuitive, which underscores the difficulty of the problem we addressed.
Having demonstrated the viability of using an algorithm based on randomisation techniques for optimising large production lines we now plan to explore other optimisation methods based on similar principles such as genetic algorithms to find how they compare to our approach. The simulated annealing algorithm can be fine-tuned in a number of ways. Results for long production lines from different approaches will allow us to tune the algorithm for optimal performance in terms of execution time and derivation of optimal results and propose prescriptive guidelines for implementing production line optimisation systems.
| \(N\) | \(S\) | \(Q\) | \(\underline{w}\) | \(R\) |
|---|---|---|---|---|
| 3 | 3 | 3 | (1.04 1.01 0.951) | 0.5478 |
| 4 | 4 | 4 | (1.06 1.01 0.976 0.95) | 0.4913 |
| 5 | 5 | 5 | (1.06 1.02 0.99 0.975 0.947) | 0.4493 |
| 6 | 6 | 6 | (1.07 1.03 1.01 0.975 0.962 0.955) | 0.4164 |
| 7 | 7 | 7 | (1.08 1.05 1.01 0.966 0.968 0.969 0.965) | 0.3898 |
| 8 | 8 | 8 | (1.09 1.04 0.98 0.998 0.973 0.983 0.97 0.962) | 0.3675 |
| 9 | 9 | 9 | (1.07 1.06 0.995 0.989 0.994 0.98 0.976 0.964 0.978) | 0.3487 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(R\) |
|---|---|---|---|---|
| 8 | 9 | 8 | ( 1 1 1 1 1 1 1 2 ) | 0.3809 |
| 8 | 10 | 8 | ( 1 1 1 1 1 1 2 2 ) | 0.3961 |
| 8 | 11 | 8 | ( 1 1 1 1 1 2 2 2 ) | 0.4122 |
| 8 | 12 | 8 | ( 1 1 1 1 2 2 2 2 ) | 0.4292 |
| 8 | 13 | 8 | ( 1 1 1 2 2 2 2 2 ) | 0.4469 |
| 8 | 14 | 8 | ( 1 1 2 2 2 2 2 2 ) | 0.4648 |
| 8 | 15 | 8 | ( 1 2 2 2 2 2 2 2 ) | 0.4831 |
| 6 | 12 | 6 | ( 2 2 2 2 2 2 ) | 0.5429 |
| 6 | 13 | 6 | ( 2 2 2 2 2 3 ) | 0.5578 |
| 4 | 25 | 4 | ( 5 6 7 7 ) | 0.8246 |
| 4 | 28 | 4 | ( 5 7 8 8 ) | 0.8415 |
| 4 | 29 | 4 | ( 5 8 8 8 ) | 0.8462 |
| 4 | 30 | 4 | ( 5 8 8 9 ) | 0.8509 |
| \(N\) | \(S\) | \(Q\) | \(\underline{s}\) | \(R\) |
|---|---|---|---|---|
| 7 | 7 | 8 | ( 1 2 1 1 1 1 1 ) | 0.421 |
| 7 | 7 | 9 | ( 1 2 1 1 1 2 1 ) | 0.4614 |
| 7 | 7 | 10 | ( 1 2 1 2 1 2 1 ) | 0.5132 |
| 7 | 7 | 11 | ( 2 2 1 2 1 2 1 ) | 0.5753 |
| 5 | 5 | 6 | ( 1 2 1 1 1 ) | 0.4992 |
| 5 | 5 | 7 | ( 1 2 1 2 1 ) | 0.5683 |
| 5 | 5 | 8 | ( 2 2 1 2 1 ) | 0.6594 |
| 5 | 5 | 9 | ( 2 2 2 2 1 ) | 0.7573 |
| 3 | 3 | 5 | ( 2 2 1 ) | 0.8051 |
| 3 | 3 | 47 | ( 27 8 12 ) | 1 |
| 3 | 3 | 92 | ( 89 1 2 ) | 1 |
| \(N\) | \(S\) | \(Q\) | \(\underline{s}\) | \(\underline{w}\) | \(R\) |
|---|---|---|---|---|---|
| 5 | 5 | 6 | ( 1 1 1 2 1 ) | (1.16 1.11 1.05 0.795 0.878) | 0.512 |
| 5 | 5 | 8 | ( 2 2 1 2 1 ) | (0.995 0.789 1.16 0.948 1.11) | 0.678 |
| 5 | 5 | 10 | ( 2 2 2 2 2 ) | (1.31 0.917 0.934 0.923 0.918) | 0.8651 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(\underline{w}\) | \(R\) |
|---|---|---|---|---|---|
| 3 | 4 | 3 | ( 1 1 2 ) | (1.08 1.04 0.885) | 0.5928 |
| 3 | 5 | 3 | ( 1 2 2 ) | (1.08 0.972 0.943) | 0.6371 |
| 3 | 6 | 3 | ( 2 2 2 ) | (1.04 0.998 0.959) | 0.6685 |
| 3 | 7 | 3 | ( 2 2 3 ) | (1.07 1 0.931) | 0.6986 |
| 3 | 8 | 3 | ( 2 3 3 ) | (1.07 0.978 0.953) | 0.7258 |
| 4 | 5 | 4 | ( 1 1 1 2 ) | (1.09 1.04 1 0.862) | 0.5258 |
| 4 | 6 | 4 | ( 1 1 2 2 ) | (1.12 1.06 0.912 0.908) | 0.5598 |
| 4 | 7 | 4 | ( 1 2 2 2 ) | (1.09 0.988 0.957 0.961) | 0.5926 |
| 4 | 8 | 4 | ( 2 2 2 2 ) | (1.06 1 0.977 0.966) | 0.6157 |
| 4 | 9 | 4 | ( 2 2 2 3 ) | (1.07 1.02 0.998 0.914) | 0.6397 |
| 4 | 10 | 4 | ( 2 2 3 3 ) | (1.09 1.02 0.945 0.938) | 0.6621 |
| 5 | 6 | 5 | ( 1 1 1 1 2 ) | (1.1 1.06 1.02 0.986 0.834) | 0.477 |
| 5 | 7 | 5 | ( 1 1 1 2 2 ) | (1.12 1.08 1.02 0.895 0.877) | 0.5049 |
| 5 | 8 | 5 | ( 1 1 2 2 2 ) | (1.14 1.07 0.944 0.925 0.917) | 0.5319 |
| 5 | 9 | 5 | ( 1 2 2 2 2 ) | (1.12 1 0.965 0.968 0.944) | 0.5577 |
| 5 | 10 | 5 | ( 1 2 2 2 3 ) | (1.14 1.01 0.991 0.97 0.889) | 0.5764 |
| 5 | 11 | 5 | ( 2 2 2 2 3 ) | (1.08 1.03 1.01 0.985 0.899) | 0.5956 |
| 5 | 12 | 5 | ( 2 2 2 3 3 ) | (1.09 1.03 1.01 0.932 0.927) | 0.6147 |
| 5 | 13 | 5 | ( 2 2 3 3 3 ) | (1.1 1.04 0.956 0.962 0.947) | 0.6324 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(\underline{s}\) | \(R\) |
|---|---|---|---|---|---|
| 3 | 3 | 4 | ( 1 1 1 ) | ( 1 2 1 ) | 0.6487 |
| 3 | 4 | 4 | ( 2 1 1 ) | ( 1 2 1 ) | 0.6918 |
| 3 | 5 | 4 | ( 2 2 1 ) | ( 1 2 1 ) | 0.7329 |
| 3 | 6 | 4 | ( 2 2 2 ) | ( 1 2 1 ) | 0.7647 |
| 3 | 7 | 4 | ( 3 2 2 ) | ( 1 2 1 ) | 0.7906 |
| 3 | 3 | 5 | ( 1 1 1 ) | ( 2 2 1 ) | 0.8051 |
| 3 | 4 | 5 | ( 1 1 2 ) | ( 2 2 1 ) | 0.8447 |
| 3 | 5 | 5 | ( 1 1 3 ) | ( 2 2 1 ) | 0.8698 |
| 3 | 6 | 5 | ( 1 1 4 ) | ( 2 2 1 ) | 0.8872 |
| 3 | 7 | 5 | ( 1 1 5 ) | ( 2 2 1 ) | 0.8999 |
| 3 | 4 | 6 | ( 2 1 1 ) | ( 2 2 2 ) | 1.037 |
| 3 | 5 | 6 | ( 3 1 1 ) | ( 2 2 2 ) | 1.09 |
| 3 | 6 | 6 | ( 3 1 2 ) | ( 2 2 2 ) | 1.134 |
| 3 | 7 | 6 | ( 3 2 2 ) | ( 2 2 2 ) | 1.181 |
| 4 | 5 | 5 | ( 1 1 1 2 ) | ( 1 2 1 1 ) | 0.6008 |
| 4 | 6 | 5 | ( 2 1 1 2 ) | ( 1 2 1 1 ) | 0.6323 |
| 4 | 7 | 5 | ( 2 2 1 2 ) | ( 1 2 1 1 ) | 0.6607 |
| 4 | 8 | 5 | ( 2 2 1 3 ) | ( 1 2 1 1 ) | 0.687 |
| 4 | 5 | 6 | ( 1 1 1 2 ) | ( 2 2 1 1 ) | 0.7065 |
| 4 | 6 | 6 | ( 1 1 1 3 ) | ( 2 2 1 1 ) | 0.7385 |
| 4 | 7 | 6 | ( 1 1 2 3 ) | ( 2 2 1 1 ) | 0.7648 |
| 4 | 8 | 6 | ( 1 1 2 4 ) | ( 2 2 1 1 ) | 0.786 |
| 4 | 5 | 7 | ( 1 1 1 2 ) | ( 2 2 2 1 ) | 0.817 |
| 4 | 6 | 7 | ( 1 1 1 3 ) | ( 2 2 2 1 ) | 0.8403 |
| 4 | 7 | 7 | ( 1 1 2 3 ) | ( 2 2 2 1 ) | 0.8569 |
| 4 | 8 | 7 | ( 1 2 2 3 ) | ( 2 2 2 1 ) | 0.8737 |
| 4 | 5 | 8 | ( 2 1 1 1 ) | ( 2 2 2 2 ) | 0.9762 |
| 4 | 6 | 8 | ( 3 1 1 1 ) | ( 2 2 2 2 ) | 1.019 |
| 4 | 7 | 8 | ( 3 1 1 2 ) | ( 2 2 2 2 ) | 1.055 |
| 4 | 8 | 8 | ( 3 1 2 2 ) | ( 2 2 2 2 ) | 1.093 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(\underline{s}\) | \(R\) |
|---|---|---|---|---|---|
| 5 | 6 | 6 | ( 1 1 1 1 2 ) | ( 1 2 1 1 1 ) | 0.5304 |
| 5 | 7 | 6 | ( 1 2 1 1 2 ) | ( 1 1 2 1 1 ) | 0.5603 |
| 5 | 8 | 6 | ( 2 1 1 2 2 ) | ( 1 2 1 1 1 ) | 0.5884 |
| 5 | 9 | 6 | ( 2 2 1 2 2 ) | ( 1 2 1 1 1 ) | 0.6097 |
| 5 | 6 | 7 | ( 1 1 1 1 2 ) | ( 2 2 1 1 1 ) | 0.5984 |
| 5 | 7 | 7 | ( 1 1 1 2 2 ) | ( 2 2 1 1 1 ) | 0.6426 |
| 5 | 8 | 7 | ( 1 1 1 2 3 ) | ( 2 2 1 1 1 ) | 0.6669 |
| 5 | 9 | 7 | ( 1 1 1 3 3 ) | ( 2 2 1 1 1 ) | 0.6913 |
| 5 | 6 | 8 | ( 1 1 1 2 1 ) | ( 2 2 1 2 1 ) | 0.6939 |
| 5 | 7 | 8 | ( 1 1 1 1 3 ) | ( 2 2 2 1 1 ) | 0.7213 |
| 5 | 8 | 8 | ( 1 1 1 2 3 ) | ( 2 2 2 1 1 ) | 0.7468 |
| 5 | 9 | 8 | ( 1 1 2 2 3 ) | ( 2 2 1 2 1 ) | 0.7649 |
| 5 | 6 | 9 | ( 2 1 1 1 1 ) | ( 2 2 2 2 1 ) | 0.8065 |
| 5 | 7 | 9 | ( 2 1 1 1 2 ) | ( 2 2 2 2 1 ) | 0.8463 |
| 5 | 8 | 9 | ( 2 1 1 1 3 ) | ( 2 2 2 2 1 ) | 0.8716 |
| 5 | 9 | 9 | ( 2 1 1 1 4 ) | ( 2 2 2 2 1 ) | 0.889 |
| 5 | 6 | 10 | ( 2 1 1 1 1 ) | ( 2 2 2 2 2 ) | 0.9262 |
| 5 | 7 | 10 | ( 3 1 1 1 1 ) | ( 2 2 2 2 2 ) | 0.9611 |
| 5 | 8 | 10 | ( 3 1 1 1 2 ) | ( 2 2 2 2 2 ) | 0.9916 |
| 5 | 9 | 10 | ( 3 1 1 2 2 ) | ( 2 2 2 2 2 ) | 1.024 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(\underline{s}\) | \(\underline{w}\) | \(R\) |
|---|---|---|---|---|---|---|
| 3 | 4 | 4 | ( 1 2 1 ) | ( 1 2 1 ) | (1.2 0.778 1.02) | 0.7228 |
| 3 | 5 | 4 | ( 2 2 1 ) | ( 1 2 1 ) | (1.16 0.789 1.05) | 0.7686 |
| 3 | 6 | 4 | ( 2 2 2 ) | ( 1 2 1 ) | (1.2 0.767 1.04) | 0.8052 |
| 3 | 7 | 4 | ( 2 3 2 ) | ( 1 2 1 ) | (1.19 0.773 1.04) | 0.8317 |
| 3 | 4 | 5 | ( 2 1 1 ) | ( 2 2 1 ) | (0.913 0.823 1.26) | 0.9071 |
| 3 | 5 | 5 | ( 2 1 2 ) | ( 2 2 1 ) | (0.93 0.836 1.23) | 0.9481 |
| 3 | 6 | 5 | ( 3 1 2 ) | ( 2 2 1 ) | (0.874 0.859 1.27) | 0.9881 |
| 3 | 7 | 5 | ( 3 2 2 ) | ( 2 2 1 ) | (0.883 0.802 1.31) | 1.027 |
| 3 | 4 | 6 | ( 2 1 1 ) | ( 2 2 2 ) | (1.09 0.964 0.948) | 1.041 |
| 3 | 5 | 6 | ( 3 1 1 ) | ( 2 2 2 ) | (1.02 0.994 0.987) | 1.091 |
| 3 | 6 | 6 | ( 3 1 2 ) | ( 2 2 2 ) | (1.06 1.03 0.914) | 1.139 |
| 3 | 7 | 6 | ( 3 2 2 ) | ( 2 2 2 ) | (1.09 0.96 0.954) | 1.185 |
| 4 | 5 | 5 | ( 1 1 1 2 ) | ( 1 2 1 1 ) | (1.22 0.804 0.989 0.983) | 0.6161 |
| 4 | 6 | 5 | ( 1 2 2 1 ) | ( 1 1 2 1 ) | (1.19 1.04 0.778 0.99) | 0.6515 |
| 4 | 7 | 5 | ( 2 2 2 1 ) | ( 1 1 2 1 ) | (1.15 1.07 0.767 1.02) | 0.6833 |
| 4 | 8 | 5 | ( 2 2 2 2 ) | ( 1 1 2 1 ) | (1.16 1.09 0.772 0.971) | 0.7103 |
| 4 | 5 | 6 | ( 1 1 2 1 ) | ( 2 1 2 1 ) | (0.95 1.15 0.797 1.11) | 0.7299 |
| 4 | 6 | 6 | ( 2 2 1 1 ) | ( 1 2 2 1 ) | (1.27 0.794 0.797 1.14) | 0.7681 |
| 4 | 7 | 6 | ( 2 2 1 2 ) | ( 1 2 2 1 ) | (1.31 0.798 0.791 1.1) | 0.7997 |
| 4 | 8 | 6 | ( 2 1 3 2 ) | ( 2 1 2 1 ) | (0.86 1.21 0.798 1.13) | 0.8367 |
| 4 | 5 | 7 | ( 2 1 1 1 ) | ( 2 2 2 1 ) | (0.965 0.853 0.862 1.32) | 0.8766 |
| 4 | 6 | 7 | ( 2 1 1 2 ) | ( 2 2 2 1 ) | (0.988 0.883 0.869 1.26) | 0.9121 |
| 4 | 7 | 7 | ( 3 1 1 2 ) | ( 2 2 2 1 ) | (0.923 0.897 0.894 1.29) | 0.9449 |
| 4 | 8 | 7 | ( 2 1 3 2 ) | ( 2 1 2 2 ) | (1.01 1.39 0.803 0.801) | 0.9404 |
| 5 | 6 | 6 | ( 1 1 1 1 2 ) | ( 1 1 2 1 1 ) | (1.19 1.14 0.796 0.932 0.94) | 0.5438 |
| 5 | 7 | 6 | ( 1 1 1 2 2 ) | ( 1 2 1 1 1 ) | (1.23 0.809 0.986 0.99 0.983) | 0.5759 |
| 5 | 6 | 7 | ( 1 1 2 1 1 ) | ( 1 1 2 2 1 ) | (1.3 1.19 0.743 0.748 1.02) | 0.6226 |
| 5 | 7 | 7 | ( 1 2 2 1 1 ) | ( 1 1 2 2 1 ) | (1.27 1.1 0.788 0.786 1.06) | 0.6556 |
| 5 | 6 | 8 | ( 1 2 1 1 1 ) | ( 1 2 2 2 1 ) | (1.43 0.803 0.796 0.8 1.17) | 0.7202 |
| 5 | 7 | 8 | ( 2 1 1 1 2 ) | ( 2 2 2 1 1 ) | (0.908 0.809 0.801 1.24 1.24) | 0.769 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(R\) |
|---|---|---|---|---|
| 8 | 9 | 8 | ( 1 1 1 1 1 1 1 2 ) | 0.3809 |
| 8 | 10 | 8 | ( 1 1 1 1 1 1 2 2 ) | 0.3961 |
| 8 | 11 | 8 | ( 1 1 1 1 1 2 2 2 ) | 0.4122 |
| 8 | 12 | 8 | ( 1 1 1 1 2 2 2 2 ) | 0.4292 |
| 8 | 13 | 8 | ( 1 1 1 2 2 2 2 2 ) | 0.4469 |
| 8 | 14 | 8 | ( 1 1 2 2 2 2 2 2 ) | 0.4648 |
| 8 | 15 | 8 | ( 1 2 2 2 2 2 2 2 ) | 0.4831 |
| 6 | 12 | 6 | ( 2 2 2 2 2 2 ) | 0.5429 |
| 6 | 13 | 6 | ( 2 2 2 2 2 3 ) | 0.5578 |
| 4 | 25 | 4 | ( 5 6 7 7 ) | 0.8246 |
| 4 | 28 | 4 | ( 5 7 8 8 ) | 0.8415 |
| 4 | 29 | 4 | ( 5 8 8 8 ) | 0.8462 |
| 4 | 30 | 4 | ( 5 8 8 9 ) | 0.8509 |
| \(N\) | \(S\) | \(Q\) | \(\underline{s}\) | \(R\) |
|---|---|---|---|---|
| 7 | 7 | 8 | ( 1 2 1 1 1 1 1 ) | 0.421 |
| 7 | 7 | 9 | ( 1 2 1 1 1 2 1 ) | 0.4614 |
| 7 | 7 | 10 | ( 1 2 1 2 1 2 1 ) | 0.5132 |
| 7 | 7 | 11 | ( 2 2 1 2 1 2 1 ) | 0.5753 |
| 5 | 5 | 6 | ( 1 2 1 1 1 ) | 0.4992 |
| 5 | 5 | 7 | ( 1 2 1 2 1 ) | 0.5683 |
| 5 | 5 | 8 | ( 2 2 1 2 1 ) | 0.6594 |
| 5 | 5 | 9 | ( 2 2 2 2 1 ) | 0.7573 |
| 3 | 3 | 5 | ( 2 2 1 ) | 0.8051 |
| 3 | 3 | 47 | ( 15 15 17 ) | 4.109e+004 |
| 3 | 3 | 92 | ( 29 32 31 ) | 41.89 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(\underline{s}\) | \(R\) |
|---|---|---|---|---|---|
| 3 | 4 | 4 | ( 2 1 1 ) | ( 1 2 1 ) | 0.6918 |
| 3 | 5 | 4 | ( 2 2 1 ) | ( 1 2 1 ) | 0.7329 |
| 3 | 6 | 4 | ( 2 2 2 ) | ( 1 2 1 ) | 0.7647 |
| 3 | 7 | 4 | ( 3 2 2 ) | ( 1 2 1 ) | 0.7906 |
| 3 | 4 | 5 | ( 1 1 2 ) | ( 2 2 1 ) | 0.8447 |
| 3 | 5 | 5 | ( 1 1 3 ) | ( 2 2 1 ) | 0.8698 |
| 3 | 6 | 5 | ( 1 1 4 ) | ( 2 2 1 ) | 0.8872 |
| 3 | 7 | 5 | ( 1 1 5 ) | ( 2 2 1 ) | 0.8999 |
| 3 | 4 | 6 | ( 2 1 1 ) | ( 2 2 2 ) | 1.037 |
| 3 | 5 | 6 | ( 3 1 1 ) | ( 2 2 2 ) | 1.09 |
| 3 | 6 | 6 | ( 3 1 2 ) | ( 2 2 2 ) | 1.134 |
| 3 | 7 | 6 | ( 3 2 2 ) | ( 2 2 2 ) | 1.181 |
| 4 | 5 | 5 | ( 1 1 1 2 ) | ( 1 2 1 1 ) | 0.6008 |
| 4 | 6 | 5 | ( 2 1 1 2 ) | ( 1 2 1 1 ) | 0.6323 |
| 4 | 7 | 5 | ( 2 2 1 2 ) | ( 1 2 1 1 ) | 0.6607 |
| 4 | 8 | 5 | ( 2 2 1 3 ) | ( 1 2 1 1 ) | 0.687 |
| 4 | 5 | 6 | ( 1 1 1 2 ) | ( 2 2 1 1 ) | 0.7065 |
| 4 | 6 | 6 | ( 1 1 1 3 ) | ( 2 2 1 1 ) | 0.7385 |
| 4 | 7 | 6 | ( 1 1 2 3 ) | ( 2 2 1 1 ) | 0.7648 |
| 4 | 8 | 6 | ( 1 1 2 4 ) | ( 2 2 1 1 ) | 0.786 |
| 4 | 5 | 7 | ( 1 1 1 2 ) | ( 2 2 2 1 ) | 0.817 |
| 4 | 6 | 7 | ( 1 1 1 3 ) | ( 2 2 2 1 ) | 0.8403 |
| 4 | 7 | 7 | ( 1 1 2 3 ) | ( 2 2 2 1 ) | 0.8569 |
| 4 | 8 | 7 | ( 1 2 2 3 ) | ( 2 2 2 1 ) | 0.8737 |
| 4 | 5 | 8 | ( 2 1 1 1 ) | ( 2 2 2 2 ) | 0.9762 |
| 4 | 6 | 8 | ( 3 1 1 1 ) | ( 2 2 2 2 ) | 1.019 |
| 4 | 7 | 8 | ( 3 1 1 2 ) | ( 2 2 2 2 ) | 1.055 |
| 4 | 8 | 8 | ( 3 1 2 2 ) | ( 2 2 2 2 ) | 1.093 |
| \(N\) | \(S\) | \(Q\) | \(\underline{q}\) | \(\underline{s}\) | \(R\) |
|---|---|---|---|---|---|
| 5 | 6 | 6 | ( 1 1 1 1 2 ) | ( 1 2 1 1 1 ) | 0.5304 |
| 5 | 7 | 6 | ( 1 1 1 2 2 ) | ( 1 2 1 1 1 ) | 0.5639 |
| 5 | 8 | 6 | ( 2 1 1 2 2 ) | ( 1 2 1 1 1 ) | 0.5884 |
| 5 | 9 | 6 | ( 2 2 1 2 2 ) | ( 1 2 1 1 1 ) | 0.6097 |
| 5 | 6 | 7 | ( 1 1 1 1 2 ) | ( 2 2 1 1 1 ) | 0.5984 |
| 5 | 7 | 7 | ( 1 1 1 2 2 ) | ( 2 2 1 1 1 ) | 0.6426 |
| 5 | 8 | 7 | ( 1 1 1 2 3 ) | ( 2 2 1 1 1 ) | 0.6669 |
| 5 | 9 | 7 | ( 1 1 1 3 3 ) | ( 2 2 1 1 1 ) | 0.6913 |
| 5 | 6 | 8 | ( 1 1 1 2 1 ) | ( 2 2 1 2 1 ) | 0.6939 |
| 5 | 7 | 8 | ( 1 1 1 2 2 ) | ( 2 2 1 2 1 ) | 0.7218 |
| 5 | 8 | 8 | ( 1 1 1 2 3 ) | ( 2 2 2 1 1 ) | 0.7468 |
| 5 | 9 | 8 | ( 1 1 1 2 4 ) | ( 2 2 2 1 1 ) | 0.7665 |
| 5 | 6 | 9 | ( 2 1 1 1 1 ) | ( 2 2 2 2 1 ) | 0.8065 |
| 5 | 7 | 9 | ( 2 1 1 1 2 ) | ( 2 2 2 2 1 ) | 0.8463 |
| 5 | 8 | 9 | ( 2 1 1 1 3 ) | ( 2 2 2 2 1 ) | 0.8716 |
| 5 | 9 | 9 | ( 2 1 1 1 4 ) | ( 2 2 2 2 1 ) | 0.889 |
| 5 | 6 | 10 | ( 2 1 1 1 1 ) | ( 2 2 2 2 2 ) | 0.9262 |
| 5 | 7 | 10 | ( 3 1 1 1 1 ) | ( 2 2 2 2 2 ) | 0.9611 |
| 5 | 8 | 10 | ( 3 1 1 1 2 ) | ( 2 2 2 2 2 ) | 0.9916 |
| 5 | 9 | 10 | ( 3 1 1 2 2 ) | ( 2 2 2 2 2 ) | 1.024 |
| \(Q\) | \(\underline{q}\) | \(R\) | \(T\) |
|---|---|---|---|
| 11 | 1 1 1 1 1 1 1 2 2 | 0.3735 | 311 |
| 12 | 1 1 1 1 1 1 2 2 2 | 0.3876 | 299 |
| 13 | 1 1 1 1 1 2 2 2 2 | 0.4024 | 282 |
| 14 | 1 1 1 1 2 2 2 2 2 | 0.4179 | 291 |
| 15 | 1 1 1 2 2 2 2 2 2 | 0.4337 | 287 |
| 16 | 1 1 2 2 2 2 2 2 2 | 0.4496 | 491 |
| 17 | 1 2 2 2 2 2 2 2 2 | 0.4658 | 135 |
| 18 | 2 2 2 2 2 2 2 2 2 | 0.4761 | 338 |
| 19 | 2 2 2 2 2 2 2 2 3 | 0.4861 | 429 |
| 20 | 2 2 2 2 2 2 2 3 3 | 0.4964 | 374 |
| 21 | 2 2 2 2 2 2 3 3 3 | 0.5071 | 342 |
| \(Q\) | \(\underline{q}\) | \(R\) | \(T\) |
|---|---|---|---|
| 11 | 1 1 1 1 1 1 1 2 2 | 0.3735 | 1 |
| 12 | 1 1 1 1 1 1 2 2 2 | 0.3876 | 2 |
| 13 | 1 1 1 1 1 2 2 2 2 | 0.4024 | 6 |
| 14 | 1 1 1 1 2 2 2 2 2 | 0.4179 | 15 |
| 15 | 1 1 1 2 2 2 2 2 2 | 0.4337 | 37 |
| 16 | 1 1 2 2 2 2 2 2 2 | 0.4496 | 78 |
| 17 | 1 2 2 2 2 2 2 2 2 | 0.4658 | 155 |
| 18 | 2 2 2 2 2 2 2 2 2 | 0.4761 | 294 |
| \(Q\) | \(\underline{q}\) | \(R\) | \(T\) |
|---|---|---|---|
| 16 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 | 0.281 | 843 |
| 17 | 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 | 0.288 | 817 |
| 18 | 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 | 0.2954 | 880 |
| 19 | 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 | 0.3031 | 849 |
| 20 | 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 | 0.3113 | 870 |
| 21 | 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 | 0.3198 | 836 |
| 22 | 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 | 0.3287 | 705 |
| 23 | 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 | 0.338 | 748 |
| 24 | 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 | 0.3475 | 763 |
| 25 | 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 | 0.3572 | 862 |
| 26 | 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 | 0.3669 | 819 |
| 27 | 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 | 0.3765 | 740 |
| 28 | 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.3858 | 1326 |
| 29 | 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.3947 | 425 |
| 30 | 1 2 2 2 2 2 2 2 2 2 2 2 2 2 3 | 0.4003 | 1290 |
| 31 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 | 0.406 | 1442 |
| 32 | 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 | 0.412 | 1196 |
| 33 | 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 | 0.4182 | 1155 |
| 34 | 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 | 0.4246 | 1059 |
| 35 | 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 | 0.4311 | 1000 |
| 36 | 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 | 0.4378 | 1009 |
| 37 | 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 | 0.4446 | 881 |
| 38 | 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 | 0.4514 | 869 |
| 39 | 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 | 0.4582 | 815 |
| 40 | 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 | 0.465 | 785 |
| 41 | 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 | 0.4716 | 830 |
| 42 | 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 | 0.4779 | 852 |
| 43 | 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 | 0.4837 | 748 |
| 44 | 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 | 0.489 | 803 |
| 45 | 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 | 0.4937 | 1051 |
| \(Q\) | \(\underline{q}\) | \(R\) | \(T\) |
|---|---|---|---|
| 16 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 | 0.281 | 0 |
| 17 | 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 | 0.288 | 2 |
| 18 | 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 | 0.2954 | 12 |
| 19 | 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 | 0.3031 | 54 |
| 20 | 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 | 0.3113 | 208 |
[p]
| \(N\) | \(\underline{q}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | 3 1 2 2 | 1.093 | 55 |
| 5 | 3 1 2 2 2 | 1.057 | 100 |
| 6 | 3 1 2 2 2 2 | 1.025 | 132 |
| 7 | 3 1 2 2 2 2 2 | 0.9976 | 170 |
| 8 | 3 1 2 2 2 2 2 2 | 0.9728 | 235 |
| 10 | 3 1 2 2 2 2 2 2 2 2 | 0.93 | 347 |
| 20 | 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7932 | 1315 |
| 30 | 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7152 | 2313 |
| 40 | 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6626 | 4174 |
| 50 | 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6237 | 6495 |
| 60 | 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.5933 | 10075 |
[p]
| \(N\) | \(\underline{q}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | 2 2 2 2 | 1.077 | 1 |
| 5 | 2 2 2 2 2 | 1.043 | 1 |
[p]
| \(N\) | \(\underline{w}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | 1.2 0.933 0.943 0.926 | 1.09 | 103 |
| 5 | 1.21 0.943 0.942 0.946 0.959 | 1.056 | 148 |
| 6 | 1.23 0.958 0.958 0.963 0.946 0.947 | 1.025 | 193 |
| 7 | 1.23 0.961 0.957 0.968 0.957 0.962 0.966 | 0.9974 | 255 |
| 8 | 1.23 0.951 0.967 0.962 0.965 0.976 0.972 0.974 | 0.9727 | 316 |
| 10 | 1.24 0.978 0.982 0.972 0.964 0.983 0.97 0.968 0.967 0.974 | 0.9301 | 465 |
| 20 | 1.26 1 0.996 0.988 0.981 0.982 0.975 0.981 0.973 0.991 0.987 1 0.983 0.995 0.985 0.987 0.979 0.987 0.984 0.984 | 0.7933 | 1501 |
| 30 | 1.27 0.971 0.974 0.989 0.985 0.978 0.992 0.974 1 0.986 0.996 0.983 0.976 0.983 0.981 0.984 0.99 0.998 1.01 1.02 0.988 0.986 1 0.982 1.01 0.984 0.984 1.01 1.01 1 | 0.7153 | 2822 |
| 40 | 1.26 0.977 1 0.994 0.995 0.968 0.976 1.02 1 1.01 0.984 0.988 1 0.985 1.01 0.982 0.988 0.984 1.01 0.98 0.991 0.991 0.994 1 0.98 0.991 0.998 0.997 0.985 1.02 1.01 0.987 1.01 0.987 1.01 0.997 1.02 0.982 0.981 0.973 | 0.6625 | 4501 |
| 50 | 1.26 1 0.988 0.985 0.994 0.998 0.964 0.975 0.998 1 0.986 0.956 0.97 1 0.977 1.03 0.993 0.982 0.969 0.98 1.01 0.988 0.997 0.996 0.998 0.994 1 1 1.01 0.994 1.01 0.979 0.99 0.997 1.01 0.995 0.981 0.98 0.982 1.02 0.973 1.01 1.03 1.01 1.01 1.01 1.01 0.986 1.01 0.991 | 0.6235 | 6389 |
| 60 | 1.28 0.972 0.964 0.966 0.968 0.972 1.02 0.973 1.02 1 0.983 0.98 0.989 0.997 0.977 0.992 0.982 0.98 1.02 0.948 1 0.968 0.989 1.06 1.01 0.994 1.03 0.96 0.995 1.01 1 1.08 0.981 0.967 0.995 1.03 1.01 0.998 1.02 0.991 0.975 0.988 0.986 0.961 1.01 1.02 1.01 0.99 0.976 0.984 1.01 0.997 1.01 0.994 1 1 1 0.983 1.01 1.02 | 0.5928 | 11659 |
[p]
| \(N\) | \(\underline{s}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | 2 2 2 2 | 1.077 | 21 |
| 5 | 2 2 2 2 2 | 1.043 | 25 |
| 6 | 2 2 2 2 2 2 | 1.013 | 32 |
| 7 | 2 2 2 2 2 2 2 | 0.9866 | 44 |
| 8 | 2 2 2 2 2 2 2 2 | 0.9629 | 60 |
| 10 | 2 2 2 2 2 2 2 2 2 2 | 0.9218 | 124 |
| 20 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.789 | 460 |
| 30 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7126 | 920 |
| 40 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6607 | 1867 |
| 50 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6223 | 2788 |
| 60 | 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.5921 | 4915 |
[p]
| \(N\) | \(\underline{s}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | 2 2 2 2 | 1.077 | 1 |
| 5 | 2 2 2 2 2 | 1.043 | 26 |
[p]
| \(N\) | \(\underline{q}\), \(\underline{w}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | \(\underline{q}\): 3 1 2 2 | 1.098 | 126 |
| \(\underline{w}\): 1.08 1.05 0.936 0.935 | |||
| 5 | \(\underline{q}\): 3 1 2 2 2 | 1.062 | 181 |
| \(\underline{w}\): 1.08 1.07 0.949 0.959 0.938 | |||
| 6 | \(\underline{q}\): 3 1 2 2 2 2 | 1.031 | 244 |
| \(\underline{w}\): 1.1 1.07 0.96 0.943 0.965 0.961 | |||
| 7 | \(\underline{q}\): 3 1 2 2 2 2 2 | 1.003 | 319 |
| \(\underline{w}\): 1.11 1.07 0.965 0.958 0.957 0.967 0.964 | |||
| 8 | \(\underline{q}\): 3 1 2 2 2 2 2 2 | 0.9773 | 401 |
| \(\underline{w}\): 1.12 1.07 0.979 0.972 0.963 0.958 0.972 0.969 | |||
| 10 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 | 0.9339 | 597 |
| \(\underline{w}\): 1.12 1.09 0.969 0.982 0.979 0.983 0.958 0.982 0.968 0.974 | |||
| 20 | \(\underline{q}\): 3 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7945 | 1937 |
| \(\underline{w}\): 1.11 0.975 1.09 0.984 1 0.997 0.976 0.988 1 0.974 0.992 0.988 0.997 0.979 1 0.982 0.978 0.987 0.995 0.993 | |||
| 30 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7164 | 3871 |
| \(\underline{w}\): 1.14 1.09 0.984 0.973 0.973 0.982 0.998 1 1 0.981 0.976 0.99 0.994 1 0.999 1.02 0.983 0.986 0.98 0.988 1 0.991 0.986 1 1.01 0.981 1.01 1.02 0.977 0.98 | |||
| 50 | \(\underline{q}\): 3 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 | 0.6241 | 9290 |
| \(\underline{w}\): 1.15 1.13 1.11 0.992 0.982 0.981 0.942 1.01 0.997 0.986 0.991 0.987 0.995 0.975 0.977 0.976 0.978 0.952 1 1.03 1 1.02 1.02 0.987 0.996 1.01 1 0.968 1.01 1.01 0.984 1.01 1.02 1.02 1.01 0.988 0.993 1 1.01 0.985 1 0.999 1.03 0.995 0.962 1.02 0.99 0.833 1.01 0.991 | |||
| 60 | \(\underline{q}\): 3 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.5934 | 12742 |
| \(\underline{w}\): 1.13 1.06 1.08 0.971 0.987 0.985 0.97 0.978 1.01 0.977 0.983 0.982 0.991 1 1 1.02 0.992 0.981 0.985 0.994 1.01 1.01 1.02 1 0.984 1.01 1.01 0.981 0.996 0.975 0.994 1.02 0.99 0.992 0.826 1.01 0.987 1.04 1 1.02 0.99 1.02 0.985 0.99 1 0.958 1.01 1.01 1.02 1.01 1 1.04 0.999 0.987 1.02 1.02 1.02 0.991 1.01 0.998 |
[p]
| \(N\) | \(\underline{q}\), \(\underline{s}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | \(\underline{q}\): 3 1 2 2 | 1.093 | 83 |
| \(\underline{s}\): 2 2 2 2 | |||
| 5 | \(\underline{q}\): 3 1 2 2 2 | 1.057 | 117 |
| \(\underline{s}\): 2 2 2 2 2 | |||
| 6 | \(\underline{q}\): 3 1 2 2 2 2 | 1.025 | 144 |
| \(\underline{s}\): 2 2 2 2 2 2 | |||
| 7 | \(\underline{q}\): 3 1 2 2 2 2 2 | 0.9976 | 201 |
| \(\underline{s}\): 2 2 2 2 2 2 2 | |||
| 8 | \(\underline{q}\): 3 1 2 2 2 2 2 2 | 0.9728 | 279 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 | |||
| 10 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 | 0.93 | 360 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 | |||
| 20 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7932 | 1152 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | |||
| 30 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7152 | 2434 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | |||
| 40 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6626 | 4713 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | |||
| 50 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6237 | 7244 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | |||
| 60 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.5933 | 12114 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
[p]
| \(N\) | \(\underline{q}\), \(\underline{s}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | \(\underline{q}\): 3 1 2 2 | 1.093 | 25 |
| \(\underline{s}\): 2 2 2 2 | |||
| 5 | \(\underline{q}\): 3 1 2 2 2 | 1.057 | 828 |
| \(\underline{s}\): 2 2 2 2 2 |
[p]
| \(N\) | \(\underline{s}\), \(\underline{w}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | \(\underline{s}\): 2 2 2 2 | 1.091 | 151 |
| \(\underline{w}\): 1.19 0.935 0.94 0.938 | |||
| 5 | \(\underline{s}\): 2 2 2 2 2 | 1.056 | 215 |
| \(\underline{w}\): 1.21 0.94 0.946 0.959 0.944 | |||
| 6 | \(\underline{s}\): 2 2 2 2 2 2 | 1.025 | 288 |
| \(\underline{w}\): 1.22 0.943 0.954 0.961 0.965 0.956 | |||
| 7 | \(\underline{s}\): 2 2 2 2 2 2 2 | 0.9974 | 362 |
| \(\underline{w}\): 1.22 0.948 0.977 0.958 0.969 0.959 0.966 | |||
| 8 | \(\underline{s}\): 2 2 2 2 2 2 2 2 | 0.9727 | 453 |
| \(\underline{w}\): 1.24 0.96 0.966 0.962 0.966 0.958 0.975 0.969 | |||
| 10 | \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 | 0.9301 | 746 |
| \(\underline{w}\): 1.25 0.961 0.964 0.972 0.964 0.969 0.989 0.976 0.975 0.982 | |||
| 20 | \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7933 | 2120 |
| \(\underline{w}\): 1.26 0.987 0.972 0.977 0.98 0.987 0.975 0.99 0.968 0.994 0.989 0.985 0.981 0.986 1 1 0.98 0.997 0.988 1 | |||
| 30 | \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7152 | 4326 |
| \(\underline{w}\): 1.28 0.983 0.981 0.99 0.97 0.999 0.991 0.993 0.991 1 1 0.965 0.995 0.977 0.98 0.991 0.98 1 0.984 0.977 1.01 0.988 0.991 0.994 0.993 0.96 1.03 1.01 0.994 0.997 | |||
| 50 | \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.6235 | 10130 |
| \(\underline{w}\): 1.26 0.981 0.986 0.972 0.963 0.981 0.939 0.996 0.97 0.982 0.968 0.994 0.989 0.976 0.991 0.993 1.01 1.02 1.02 0.988 0.974 1 0.987 0.978 0.979 1 1.01 1.02 1.02 0.999 0.994 0.994 0.997 0.986 1.02 1.03 1.02 1.01 1.02 1 0.988 0.982 1 0.997 1.01 1.01 0.996 0.991 0.991 1.02 | |||
| 60 | \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.593 | 13943 |
| \(\underline{w}\): 1.28 0.99 0.988 0.972 0.949 0.984 0.952 0.955 0.973 0.978 0.997 1.03 0.975 0.992 1.01 0.971 0.965 1.03 0.994 0.982 0.965 0.997 0.967 1.01 0.995 0.983 0.974 1.01 0.996 1.03 0.998 1.01 1.02 1 0.98 0.978 0.996 0.983 0.967 1 1.01 1 1 1.01 0.987 0.979 1.03 1 0.987 1 1.01 1.03 1.02 1.01 1.02 1.03 1.03 0.99 1 1.02 |
[p]
| \(N\) | \(\underline{q}\), \(\underline{s}\), \(\underline{w}\) | \(R\) | \(T\) |
|---|---|---|---|
| 4 | \(\underline{q}\): 3 1 2 2 | 1.098 | 151 |
| \(\underline{s}\): 2 2 2 2 | |||
| \(\underline{w}\): 1.07 1.05 0.934 0.945 | |||
| 5 | \(\underline{q}\): 3 1 2 2 2 | 1.062 | 218 |
| \(\underline{s}\): 2 2 2 2 2 | |||
| \(\underline{w}\): 1.1 1.06 0.951 0.95 0.941 | |||
| 6 | \(\underline{q}\): 3 1 2 2 2 2 | 1.031 | 293 |
| \(\underline{s}\): 2 2 2 2 2 2 | |||
| \(\underline{w}\): 1.1 1.06 0.955 0.958 0.962 0.958 | |||
| 7 | \(\underline{q}\): 3 1 2 2 2 2 2 | 1.003 | 376 |
| \(\underline{s}\): 2 2 2 2 2 2 2 | |||
| \(\underline{w}\): 1.11 1.07 0.966 0.962 0.963 0.964 0.961 | |||
| 8 | \(\underline{q}\): 3 1 2 2 2 2 2 2 | 0.9774 | 480 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 | |||
| \(\underline{w}\): 1.11 1.08 0.97 0.965 0.968 0.961 0.973 0.975 | |||
| 10 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 | 0.9339 | 709 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 | |||
| \(\underline{w}\): 1.11 1.08 0.977 0.98 0.955 0.975 0.984 0.973 0.98 0.982 | |||
| 20 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 3 | 0.7867 | 2332 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 1 | |||
| \(\underline{w}\): 1.12 1.09 0.97 0.975 0.956 0.984 0.972 0.965 0.964 0.97 0.976 0.983 0.972 0.969 0.983 0.963 0.974 0.794 0.989 1.43 | |||
| 30 | \(\underline{q}\): 3 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | 0.7164 | 4866 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 | |||
| \(\underline{w}\): 1.13 1.09 0.975 0.998 0.978 0.98 0.998 1.01 0.975 0.998 0.996 1.01 0.974 0.988 1.02 0.975 0.993 0.992 0.978 1.01 0.985 0.99 1 0.991 0.967 1.01 0.993 0.996 1 1.01 | |||
| 50 | \(\underline{q}\): 3 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 3 2 3 | 0.6219 | 11680 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 1 | |||
| \(\underline{w}\): 1.16 1.12 1.11 0.994 0.971 0.973 0.946 0.995 0.952 0.975 0.965 0.969 0.988 0.975 0.997 0.979 0.952 1.01 1.01 0.995 0.979 1.02 0.997 0.993 1 1.01 0.988 0.999 0.99 0.977 1.03 1.01 1.02 0.985 0.981 0.998 0.988 0.986 1.03 0.981 0.983 0.816 1.02 0.992 0.974 1.01 0.996 0.818 1 1.4 | |||
| 60 | \(\underline{q}\): 3 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 3 | 0.5919 | 16632 |
| \(\underline{s}\): 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 | |||
| \(\underline{w}\): 1.15 1.13 1.09 0.963 0.952 0.983 0.993 0.995 1 0.997 0.984 0.996 1.02 0.958 0.999 1.01 0.975 0.97 0.974 1.02 0.967 0.987 1.01 0.806 1.01 0.998 0.977 0.986 1 0.969 0.968 0.999 0.983 1.03 1.04 0.996 0.985 0.981 1.05 0.999 1.01 0.996 0.969 1.04 0.98 0.989 0.988 1.01 0.988 0.806 0.997 1.03 0.997 1.02 0.955 1.02 0.983 1 0.968 1.39 |
Altiok, T. 1982. “Approximate Analysis of Exponential Tandem Queue with Blocking.” Ejor 11: 390–398.
Altiok, T. 1997. Performance Analysis of Manufacturing Systems. New York: Springer-Verlag.
Altiok, T., and H. G. Perros. 1986. “Open Networks of Queues with Blocking: Split and Merge Configurations.” Iietrans 18: 251–261.
Altiok, T., and S. Jr. Stidham. 1983. “The Allocation of Interstage Buffer Capacities in Production Lines.” Iietrans 15 (4): 292–299.
Askin, R. G., and C. R. Standridge. 1993. Modeling and Analysis of Manufacturing Systems. New York: John Wiley.
Boxma, O., and A. Konheim. 1981. “Approximate Analysis of Exponential Queuing Systems with Blocking.” Acta 15: 19–26.
Brandwajn, A., and Y. Jow. 1988. “An Approximation Method for Tandem Queues with Blocking.” Or 36 (1): 73–83.
Buzacott, J. A., and J. G. Shanthikumar. 1992. “Design of Manufacturing Systems Using Queueing Models.” Queueing Systems 12: 135–214.
Buzacott, J. A., and J. G. Shanthikumar. 1993. Stochastic Models of Manufacturing Systems. New Jersey: Prentice Hall.
Caseau, P., and G. Pujolle. 1979. “Throughput Capacity of a Sequence of Queues with Blocking Due to Finite Waiting Room.” Ieeese 5: 631–642.
Cerny, V. 1985. “Thermodynamical Approach to the Traveling Salesman Problem: An Efficient Simulation Algorithm.” Jota 45: 41–51.
Cheah, Jenyeng, and J. MacGregor Smith. 1994. “Generalized M/G/C/C State Dependent Queueing Models and Pedestrian Traffic Flows.” Queueing Systems and Their Applications (QUESTA) 15: 365–386.
Choong, Y. F., and S. B. Gershwin. 1987. “A Decomposition Method for the Appropriate Evaluation of Capacitated Transfer Lines with Unreliable Machines and Random Processing Times.” Iietrans 19 (2): 150–159.
Conway, R., W. Maxwell, J. O. McClain, and L. J. Thomas. 1988. “The Role of Work in Process Inventory in Serial Production Lines.” Or 36 (2): 229–241.
Corana, A., M. Marchesi, C. Martini, and S. Ridella. 1987. “Minimizing Multimodal Functions of Continuous Variables with the ‘Simulated Annealing’ Algorithm.” Toms 13 (3): 262–280.
Dallery, Y., and Y. Frein. 1993. “On Decomposition Methods for Tandem Queueing Networks with Blocking.” Or 41 (2): 386–399.
Daskalaki, S., and J. MacGregor Smith. 1986. “Static Routing in Open Finite Queueing Networks.”
Daskalaki, S., and J. MacGregor Smith. 1989. “Optimal Routing and Buffer Space Allocation in Series-Parallel Queueing Networks.”
Ding, J., and B. S. Greenberg. 1991. “Bowl Shapes Are Better with Buffer — Sometimes.” Probability in the Informational and Engineering Sciences 5: 159–169.
Eglese, R. W. 1990. “Simulated Annealing: A Tool for Operational Research.” Ejor 46: 271–281.
Fredericks, A. A. 1980. “Congestion in Blocking Systems – a Simple Approximation Technique.” The Bell System Technical Journal 59 (6): 805–827.
Fredericks, A. A., and G. A. Reisner. 1979. “Approximations to Stochastic Service Systems with an Application to a Retrial Model.” The Bell System Technical Journal 58 (3): 557–576.
Gelenbe, E., and G. Pujolle. 1976. “The Behavior of a Single Queue in a General Queueing Network.” Acta 7: 123–136.
Gershwin, S. B. 1989. “An Efficient Decomposition Algorithm for Unreliable Tandem Queueing Systems with Finite Buffers.” In Queueing Networks with Blocking, edited by H. G. Perros and T. Altiok. North Holland.
Gershwin, S. B. 1994. Manufacturing Systems Engineering. New Jersey: Prentice Hall.
Glassey, C. R., and Y. Hong. 1983. “Analysis of Behaviour of an Unreliable \(n\)-Stage Transfer Line with \((n-1)\) Inter-Stage Storage Buffers.” International Journal of Production Research 31 (3): 519–530.
Glover, F. 1990. “Tabu Search — Part I.” ORSA Journal on Computing 1: 190–206.
Goldberg, David E. 1989. Genetic Algorithms: In Search of Optimization & Machine Learning. Addison-Wesley.
Gosavi, Hemant, and J. MacGregor Smith. 1990. “Heavy Traffic Multi-Commodity Routing in Open Finite Queueing Networks.”
Gun, L., and A. M. Makowski. 1989. “An Approximation Method for General Tandem Queueing Systems Subject to Blocking.” In Queueing Networks with Blocking: First International Workshop, edited by Harry G. Perros and Tayfur Altiok, 147–171. Raleigh, North Carolina, USA: North-Holland.
Gupta, R., S. A. Smolka, and S. Bhaskar. 1994. “On Randomization in Sequential and Distributed Algorithms.” Acmcs 26 (1): 7–86.
Han, Y., and J. MacGregor Smith. 1992. “Approximate Analysis of Open \(M/M/C/K\) Queueuing Networks.” In Queueing Networks with Finite Capacity: Second International Conference on Queueing Networks with Finite Capacity, edited by Raif O. Onvural and Ian F. Akyildiz, 113–126. North-Holland.
Heavey, C., H. T. Papadopoulos, and J. Browne. 1993. “The Throughput Rate of Multistation Unreliable Production Lines.” Ejor 68: 69–89.
Hillier, F. S., and R. W. Boling. 1966. “The Effect of Some Design Factors on the Efficiency of Production Lines with Variable Operation Times.” The Journal of Industrial Engineering 17: 651–658.
Hillier, F. S., and R. W. Boling. 1967. “Finite Queues in Series, with Exponential or Erlang Service Times – a Numerical Approach.” Or 15: 286–303.
Hillier, F. S., and R. W. Boling. 1977. “Toward Characterizing the Optimal Allocation of Work in Production Line Systems with Variable Operation Times.” In Advances in Operations Research, Proceedings of Second European Conference on Operations Research, edited by M. Roubens. Amsterdam: North-Holland.
Hillier, F. S., and R. W. Boling. 1979. “On the Optimal Allocation of Work in Symmetrically Unbalanced Production Line Systems with Variable Operation Times.” Management Science 25: 721–728.
Hillier, F. S., and K. C. So. 1989. “The Assignment of Extra Servers to Stations in Tandem Queueing Systems with Small or No Buffers.” Performance Evaluation 10: 219–231.
Hillier, F. S., and K. C. So. 1991a. “The Effect of Machine Breakdowns and Interstage Storage on the Performance of Production Line Systems.” International Journal of Production Research 29 (10): 2043–2055.
Hillier, F. S., and K. C. So. 1991b. “The Effect of the Coefficient of Variation of Operation Times on the Allocation of Storage Space in Production Line Systems.” Iietrans 23 (2): 198–206.
Hillier, Frederick S., and Kut C. So. 1995. “On the Optimal Design of Tandem Queueing Systems with Finite Buffers.” Queueing Systems 21: 245–266.
Himmelblau, D. M. 1972. Applied Nonlinear Programming. Mc-Graw-Hill.
Ho, Y. C., M. A. Eyler, and T. T. Chien. 1979. “A Gradient Technique for General Buffer Storage Design in a Production Line.” International Journal of Production Research 17 (2): 557–580.
Holland, J. H. 1975. Adaptation in Natural and Artificial Systems. Ann Arbor, Michigan: University of Michigan Press.
Huang, C. C., and G. Weiss. 1990. “On the Optimal Order of M Machines in Tandem.” Orl 9: 299–303.
Ingber, L. 1993. “Simulated Annealing: Practice Versus Theory.” Journal of Mathematical Computation Modelling 18 (11): 29–57.
Jafari, M. A., and J. G. Shanthikumar. 1989. “Determination of Optimal Buffer Storage Capacities and Optimal Allocation in Multistage Automatic Transfer Lines.” Iietrans 21 (2): 130–135.
Jain, Sushant, and J. MacGregor Smith. 1994. “Open Finite Queueing Networks with M/M/C/K Parallel Servers.” Comor 21 (3): 297–317.
Kerbache, L. 1984. “Analysis of Open Finite Queueing Networks.” PhD thesis, Amherst, MA 01003, USA: Department of Industrial Engineering; Operations Research, University of Massachusetts.
Kerbache, L., and J. MacGregor Smith. 1987. “The Generalized Expansion Method for Open Finite Queueing Networks.” Ejor 32: 448–461.
Kerbache, L., and J. MacGregor Smith. 1988. “Asymptotic Behaviour of the Expansion Method for Open Finite Queueing Networks.” Comor 15 (2): 157–169.
Kirkpatrick, S., C. D. Gelatt Jr., and M. P. Vecchi. 1983. “Optimization by Simulated Annealing.” Science 220: 671–679.
Kleinrock, Leonard. 1975. Queueing Systems. Vol. I: Theory. John Wiley; Sons.
Koulamas, C., S. R. Antony, and R. Jaen. 1994. “A Survey of Simulated Annealing Applications to Operations Research Problems.” Omega International Journal of Management Science 22 (1): 41–56.
Kubat, P., and U. Sumita. 1985. “Buffers and Backup Machines in Automatic Transfer Lines.” International Journal of Production Research 23 (6): 1259–1270.
Kuehn, P. J. 1979. “Approximate Analysis of General Queueing Networks by Decomposition.” IEEE Trans. on COMM 27: 113–126.
Labetoulle, J., and G. Pujolle. 1980. “Isolation Method in a Network of Queues.” Ieeese 6 (4): 373–380.
Magazine, M. J., and K. E. Stecke. 1996. “Throughput for Production Lines with Serial Work Stations and Parallel Service Facilities.” Performance Evaluation 25: 211–232.
Metropolis, N., A. N. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller. 1953. “Equation of State Calculation by Fast Computing Machines.” Jcm 21 (6): 1087–1092.
Onvural, Raif. 1990. “Survey of Closed Queueing Networks with Blocking.” Acmcs 22 (2): 83–121.
Papadopoulos, H. T., and C. Heavey. 1996. “Queueing Theory in Manufacturing Systems Analysis and Design: A Classification of Models for Production and Transfer Lines.” Ejor 92: 1–27.
Papadopoulos, H. T., C. Heavey, and J. Browne. 1993. Queueing Theory in Manufacturing Systems Analysis and Design. London: Chapman; Hall.
Perros, H. G., and T. Altiok. 1986. “Approximate Analysis of Open Networks of Queues with Blocking: Tandem Configurations.” Ieeese 12 (3): 450–461.
Powell, S. G. 1994. “Buffer Allocation in Unbalanced Three-Station Serial Lines.” International Journal of Production Research 32 (9): 2201–2217.
Press, W. H., B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling. 1988. “Numerical Recipes in C.” In, 343–352. Cambridge University Press.
Schweitzer, P., and T. Altiok. 1989. “Aggregate Modelling of Tandem Queues Without Intermediate Buffers.” In Queueing Networks with Blocking: First International Workshop, edited by Harry G. Perros and Tayfur Altiok, 47–72. Raleigh, North Carolina, USA: North-Holland.
Seong, D., S. Y. Chang, and Y. Hong. 1995. “Heuristic Algorithms for Buffer Allocation in a Production Line with Unreliable Machines.” International Journal of Production Research 33 (7): 1989–2005.
Shanthikumar, J. G., G. Yamazaki, and H. Sakasegawa. 1991. “Characterization of Optimal Order of Servers in Tandem Queue with Blocking.” Orl 10: 17–22.
Singh, A., and J. MacGregor Smith. 1997. “Buffer Allocation for an Integer Nonlinear Network Design Problem.” Comor 24 (5): 453–472.
Smith, J. MacGregor. 1991. “State Dependent Queueing Models in Emergency Evacuation Networks.” Transportation Res-B 25B (6): 373–389.
Smith, J. MacGregor. 1994. “Applications of State Dependent Queues to Pedestrian/Vehicular Network Design.” Or 42 (3): 414–427.
Smith, J. MacGregor, and Nikhil Chikhale. 1995. “Buffer Allocation for a Class of Nonlinear Stochastic Knapsack Problems.” Annals of Operations Research 58: 323–360.
Smith, J. MacGregor, and S. Daskalaki. 1988. “Buffer Space Allocation in Automated Assembly Lines.” Or 36 (2): 343–358.
Spinellis, Diomidis, and Chrisoleon T. Papadopoulos. 1997. “A Simulated Annealing Approach for Buffer Allocation in Reliable Production Lines.” In International Workshop on Performance Evaluation and Optimization of Production Lines, 365–375. Samos, Greece: University of the Aegean, Department of Mathematics. http://www.dmst.aueb.gr/dds/pubs/conf/1997-Perf-Anneal/html/anneal.html.
Takahashi, Y. 1989. “Aggregate Approximation for Acyclic Queueing Networks with Communication Blocking.” In Queueing Networks with Blocking: First International Workshop, edited by Harry G. Perros and Tayfur Altiok, 33–46. Raleigh, North Carolina, USA: North-Holland.
Takahashi, Y., H. Miyahara, and T. Hasegawa. 1980. “An Approximation Method for Open Restricted Queueing Networks.” Or 28 (3): 594–602.
Van Laarhoven, P. J. M., and E. H. L. Aarts. 1987. Simulated Annealing: Theory and Applications. Dordrecht, The Nethelands: D. Reidel.
VanDijk, N., and B. Lamond. 1988. “Simple Bounds for Finite Single Server Exponential Tandem Queues.” Or 36 (3): 470–477.
VanDijk, N., and J. van der Wal. 1989. “Simple Bounds and Monotonicity Results for Finite Multi-Server Exponential Tandem Queues.” Queueing Systems 4 (1): 1–16.
Viswanadham, N., and Y. Narahari. 1992. Performance Modeling of Automated Manufacturing Systems. New Jersey: Prentice Hall.
Wan, Y.-w., and R. W. Wolff. 1993. “Bounds for Different Arrangements of Tandem Queues with Nonoverlapping Service Times.” Management Science 39: 1173–1178.
Yamashita, H., and T. Altiok. 1997. “Buffer Capacity Allocation for a Desired Throughput in Production Lines.” In Samos International Workshop on Performance Evaluation and Optimization of Production Lines, 1–24. Samos, Greece: University of the Aegean.
Yamazaki, G., H. Sakasegawa, and J. G. Shanthikumar. 1992. “On Optimal Arrangement of Stations in a Tandem Queueing System with Blocking.” Management Science 38: 137–153.
Department of Information and Communication Systems, University of the Aegean, 83200 Karlovasi Samos, Greece. (Corresponding author); email: dspin@aegean.gr↩
Department of Business Administration, University of the Aegean, 82100 Chios, Greece. email: hpap@aegean.gr↩
Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst Massachusetts 01003, USA. email: jmsmith@ecs.umass.edu↩
International Journal of Production Research, 38(3):509–541, February 2000.↩